题目内容
18.设$\overrightarrow{m}$=(a,2),$\overrightarrow{n}$=(1,b-1),a>0,b>0,若$\overrightarrow{m}$,$\overrightarrow{n}$的夹角为$\frac{π}{2}$,则$\frac{1}{a}$+$\frac{2}{b}$的最小值是( )| A. | 无法确定 | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{9}{2}$ |
分析 由$\overrightarrow{m}•\overrightarrow{n}$=0得a+2b=2,代入$\frac{1}{a}$+$\frac{2}{b}$即可使用基本不等式解出最小值.
解答 解:∵$\overrightarrow{m}$,$\overrightarrow{n}$的夹角为$\frac{π}{2}$,∴$\overrightarrow{m}•\overrightarrow{n}$=a+2b-2=0,∴a+2b=2.
∴$\frac{1}{a}$+$\frac{2}{b}$=$\frac{a+2b}{2a}$+$\frac{a+2b}{b}$=$\frac{b}{a}$+$\frac{a}{b}$+$\frac{5}{2}$≥2+$\frac{5}{2}$=$\frac{9}{2}$.
故选:D.
点评 本题考查了向量的数量积运算,基本不等式的应用,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
5.在△ABC中,角A、B、C的对边分别是a、b、c,$\frac{asinA+bsinB-csinC}{sinBsinC}$=$\frac{2\sqrt{3}}{3}$a,a=2$\sqrt{3}$,若b∈[1,3],则c的最小值为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
6.直线l过点(0,2),被圆C:x2+y2-4x-6y+9=0截得的弦长为2$\sqrt{3}$,则直线l的方程是( )
| A. | y=$\frac{4}{3}$x+2 | B. | y=-$\frac{1}{3}$x+2 | C. | y=2 | D. | y=$\frac{4}{3}$x+2或y=2 |
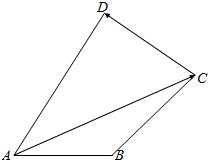 如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.