题目内容
17.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,若要使织布的总尺数不少于30尺,该女子所需的天数至少为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 由等比数列前n项和公式求出这女子每天分别织布$\frac{5}{31}$尺,由此利用等比数列前n项和公式能求出要使织布的总尺数不少于30尺,该女子所需的天数至少为多少天.
解答 解:设该女五第一天织布x尺,
则$\frac{x(1-{2}^{5})}{1-2}$=5,
解得x=$\frac{5}{31}$,
∴前n天织布的尺数为:$\frac{5}{31}({2}^{n}-1)$,
由$\frac{5}{31}({2}^{n}-1)≥$30,得2n≥187,
解得n的最小值为8.
故选:B.
点评 本题考查等比数列在生产生活中的实际应用,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
5.在△ABC中,角A、B、C的对边分别是a、b、c,$\frac{asinA+bsinB-csinC}{sinBsinC}$=$\frac{2\sqrt{3}}{3}$a,a=2$\sqrt{3}$,若b∈[1,3],则c的最小值为( )
| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
12.如果实数x,y满足条件$\left\{\begin{array}{l}{x-y-2≥0}\\{x-2≤0}\\{y+1≥0}\end{array}\right.$,则z=x+3y的最小值为-2.
2.某产品的广告费用x与销售额y的统计数据如表:
根据表格已得回归方程为$\widehat{y}$=9.4x+9.1,表中有一数据模糊不清,请推算该数据的值为37.
| 广告费x(万元) | 2 | 3 | 4 | 5 |
| 利润y(万元) | 26 |  | 49 | 56 |
9.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≤4\\ y≤2\end{array}\right.$则目标函数z=3x-y的最大值( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | -1 | D. | $-\frac{3}{2}$ |
6.直线l过点(0,2),被圆C:x2+y2-4x-6y+9=0截得的弦长为2$\sqrt{3}$,则直线l的方程是( )
| A. | y=$\frac{4}{3}$x+2 | B. | y=-$\frac{1}{3}$x+2 | C. | y=2 | D. | y=$\frac{4}{3}$x+2或y=2 |
7.已知A(2,0),B(-2,0),P(x,y),下列命题正确的是( )
| A. | 若P到A,B距离之和为4,则点P的轨迹为椭圆 | |
| B. | 若P到A,B距离之差为3,则点P的轨迹为双曲线 | |
| C. | 椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上任意一点M(长轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ | |
| D. | 双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1上任意一点M(实轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ |
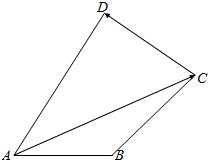 如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.
如图,四边形ABCD中,AB=1,AD=2,BC=DC,∠DAB=$\frac{π}{3}$,∠DCB=$\frac{π}{2}$,则$\overrightarrow{AC}$•$\overrightarrow{CD}$=-$\frac{\sqrt{3}}{2}$.