题目内容
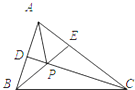△ABC中，AB=10，AC=15，∠BAC=| π |
| 3 |
| AC |
| AE |
| AP |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
考点：向量在几何中的应用
专题：平面向量及应用
分析：利用向量的关系，建立坐标系，求出相关点的坐标，然后求解向量的模即可．
解答：
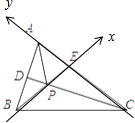解：△ABC中，AB=10，AC=15，∠BAC=
，点D是边AB的中点，点E在直线AC上，且
=3
，
可得：AE⊥BE，以BE所在直线为x轴，EA所在直线为y轴，如图：A（0，5），
BE=5
，B（-5
，0），D（-
，
），C（0，-10），
CD的方程为：
=
，令y=0，可得x=-2
，
P（-2
，0）．
|
|=
=
．
故选：A．
解：△ABC中，AB=10，AC=15，∠BAC=| π |
| 3 |
| AC |
| AE |
可得：AE⊥BE，以BE所在直线为x轴，EA所在直线为y轴，如图：A（0，5），
BE=5
| 3 |
| 3 |
5
| ||
| 2 |
| 5 |
| 2 |
CD的方程为：
y-
| ||||
x+
|
| ||||
-
|
| 3 |
P（-2
| 3 |
|
| AP |
(-2
|
| 37 |
故选：A．
点评：本题考查向量的几何中的应用，向量的坐标运算，向量的模，考查计算能力．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
若
=（sin2x，cos2x），
=（sin2x，-cos2x），f（x）=
•
+4cos2x+2
sinxcosx．如果?m∈R，对?x∈R都有f（x）≥f（m），则f（m）等于（ ）
| a |
| b |
| a |
| b |
| 3 |
A、2+2
| ||
| B、3 | ||
| C、0 | ||
D、2-2
|
已知一个几何体的三视图如图所示，那么该几何体的表面积是（ ）
A、5+
| ||
| B、7 | ||
C、7+
| ||
| D、9 |
若sin（
-α）=
，则cos（
+2α）=（ ）
| π |
| 6 |
| 1 |
| 4 |
| 2π |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|