题目内容
(1)已知函数f(x)=|x-3|+1,g(x)=kx,若函数F(x)=f(x)-g(x) 有两个零点,求k的范围.
(2)函数h(x)=
,m(x)=2x+b,若方程h(x)=m(x)有两个不等的实根,求b的取值范围.
(2)函数h(x)=
| 4-x2 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
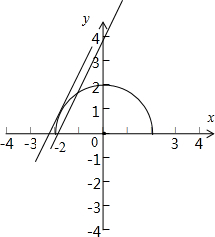
分析:(1)画出两个函数f(x)=|x-3|+1,g(x)=kx,的图象,利用函数F(x)=f(x)-g(x) 有两个零点,即可求k的范围.
(2)函数h(x)=
,m(x)=2x+b,方程h(x)=m(x)有两个不等的实根,画出图象,利用圆的切线关系求出b的取值范围.
(2)函数h(x)=
| 4-x2 |
解答:
 解:(1)因为函数F(x)=f(x)-g(x) 有两个零点,即f(x)=g(x) 有两个不等的实根
解:(1)因为函数F(x)=f(x)-g(x) 有两个零点,即f(x)=g(x) 有两个不等的实根
即函数f(x)=|x-3|+1与g(x)=kx,有两个不同的交点.
由图象得k的范围.是 (
,1).
(2)由h(x)=
,得 x2+y2=4(y≥0)即图形是以(0,0)为圆心,以2为半径的上半圆,若方程h(x)=m(x)有两个不等的实根,即两图象有两个不同的交点,
当直线m(x)=2x+b,过(-2,0)时,b=4 有两个交点,当直线与圆相切时
=2,可得b=2
,b=-2
(舍去)
b的取值范围[2,2
).
 解:(1)因为函数F(x)=f(x)-g(x) 有两个零点,即f(x)=g(x) 有两个不等的实根
解:(1)因为函数F(x)=f(x)-g(x) 有两个零点,即f(x)=g(x) 有两个不等的实根即函数f(x)=|x-3|+1与g(x)=kx,有两个不同的交点.
由图象得k的范围.是 (
| 1 |
| 3 |
(2)由h(x)=
| 4-x2 |
当直线m(x)=2x+b,过(-2,0)时,b=4 有两个交点,当直线与圆相切时
| |b| | ||
|
| 5 |
| 5 |
b的取值范围[2,2
| 5 |

点评:本题考查函数与方程的应用,考查数形结合,直线与圆的位置关系,考查分析问题解决问题的能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
若22a+1>(
)1-a成立,则a的取值范围为( )
| 1 |
| 2 |
| A、(-1,+∞) |
| B、(-2,+∞) |
| C、(-1,0) |
| D、(-∞,-2) |
已知向量
,
满足|
|=|
|=2,
与
的夹角为120°,则|
-
|的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | ||
B、2
| ||
C、3
| ||
| D、12 |
某几何体的三视图如图所示,则该几何体的表面积是( )


| A、90 | B、92 | C、98 | D、104 |
一个几何体的三视图尺寸如图,则该几何体的表面积为( )


A、4+8
| ||
| B、20 | ||
C、4+4
| ||
| D、12 |
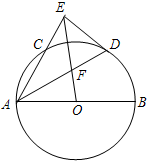 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若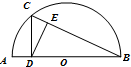 如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=
如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=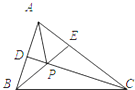 △ABC中,AB=10,AC=15,∠BAC=
△ABC中,AB=10,AC=15,∠BAC=