题目内容
设向量
,
满足|
|=
,|
|=3,x是
在
的方向上的正射影的数量,则函数y=|
|x的值域是 .
| a |
| b |
| a |
| 1 |
| 2 |
| b |
| b |
| a |
| a |
考点:平面向量数量积的运算
专题:计算题,函数的性质及应用,平面向量及应用
分析:由题意知,向量
在
方向上的射影的数量是x=|
|•cosθ,且θ∈[0,π],所以x∈[-3,3],则函数y的最大值为(
)-3=8,最小值为(
)3=
,值域可求.
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
解答:
解:∵向量
,
的夹角为θ,且|
|=
,|
|=3,
∴向量
在
方向上的射影的数量是:x=|
|•cosθ=3cosθ,
又∵0≤θ≤π,∴-1≤cosθ≤1,∴-3≤x≤3;
由于y=(
)x在R上递减,
则函数y=|
|x的最大值为(
)-3=8,最小值为(
)3=
,
则函数y的值域为[
,8].
故答案为:[
,8].
| a |
| b |
| a |
| 1 |
| 2 |
| b |
∴向量
| b |
| a |
| b |
又∵0≤θ≤π,∴-1≤cosθ≤1,∴-3≤x≤3;
由于y=(
| 1 |
| 2 |
则函数y=|
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
则函数y的值域为[
| 1 |
| 8 |
故答案为:[
| 1 |
| 8 |
点评:本题考查了平面向量中一向量在另一向量方向上的射影,向量的夹角,指数函数的单调性的运用等概念,是基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
设f(x)=lg(
+a)是奇函数,则a的取值( )
| 2 |
| 1+x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
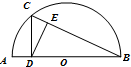 如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=
如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=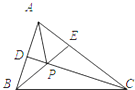 △ABC中,AB=10,AC=15,∠BAC=
△ABC中,AB=10,AC=15,∠BAC=