题目内容
已知函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
(1)求实数m,n的值
(2)用定义证明f(x)在(-1,1)上是增函数.
| mx+n |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)求实数m,n的值
(2)用定义证明f(x)在(-1,1)上是增函数.
考点:函数单调性的判断与证明,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)奇函数在原点有定义时,f(0)=0,从而可求得n=0,而由f(
)=
可求出m;
(2)根据增函数的定义,设x1,x2∈(-1,1),且x1<x2,通过作差的方法证明f(x1)<f(x2)即可.
| 1 |
| 2 |
| 2 |
| 5 |
(2)根据增函数的定义,设x1,x2∈(-1,1),且x1<x2,通过作差的方法证明f(x1)<f(x2)即可.
解答:
解:(1)∵f(x)为(-1,1)上的奇函数
∴f(0)=0;
∴n=0;
∵f(
)=
;
∴
=
;
∴m=1;
(2)f(x)=
;
设x1,x2∈(-1,1),且x1<x2,则:
f(x1)-f(x2)=
-
=
;
∵x1,x2∈(-1,1),且x1<x2;
∴x1-x2<0,1-x1x2>0;
∴f(x1)<f(x2);
∴f(x)在(-1,1)上是增函数.
∴f(0)=0;
∴n=0;
∵f(
| 1 |
| 2 |
| 2 |
| 5 |
∴
| ||
|
| 2 |
| 5 |
∴m=1;
(2)f(x)=
| x |
| 1+x2 |
设x1,x2∈(-1,1),且x1<x2,则:
f(x1)-f(x2)=
| x1 |
| 1+x12 |
| x2 |
| 1+x22 |
| (x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
∵x1,x2∈(-1,1),且x1<x2;
∴x1-x2<0,1-x1x2>0;
∴f(x1)<f(x2);
∴f(x)在(-1,1)上是增函数.
点评:考查奇函数的定义,以及根据增函数的定义证明函数为增函数的方法与过程.

练习册系列答案
相关题目
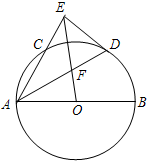 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若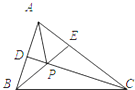 △ABC中,AB=10,AC=15,∠BAC=
△ABC中,AB=10,AC=15,∠BAC=