题目内容
已知实数a满足有且仅有一个正方形,其四个顶点均在曲线y=x3+ax上,求该正方形的边长.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:三角函数的求值
分析:分别设出A,B,C,D的坐标,令x0=rcosθ,y0=rsinθ,r>0,θ∈(0,
),得到方程(1+a2)(sin22θ)2-(4+a2)sin22θ+4=0,根据△=0,解出即可.
| π |
| 2 |
解答:
解:设正方形的四个顶点为 A、B、C、D,那么ABCD的中心为原点O.
否则,由于y=x3+ax为奇函数,因此A、B、C、D关于O点的对称点A′、B′、C′、D′也在曲线上,
且A′B′C′D′也是正方形,与题设矛盾.设四点为A(x0,y0),B(-y0,x0),C(-x0,-y0),D(y0,-x0),其中x0>0,y0>0,
则y0=x03+ax0,①,-x0=y03+ay0,②,
①×x0+②×y0,得:x04+y04+a(x02+y02)=0,③
①×y0-②×x0,得:x02+y02=x0y0(x02-y02),④
令x0=rcosθ,y0=rsinθ,r>0,θ∈(0,
),
由③④得:a=-r2(1-2sin2θcos2θ)
消去r2,得关于sin2θ的方程:
(1+a2)(sin22θ)2-(4+a2)sin22θ+4=0
因sin22θ在(0,1)内只有一个根,
∴△=(a2+4)2-16(1+a2)=a4-8a2=0,
∴a=-2
,(由③知a<0),sin2θ=
,sin4θ=
,r=
,
∴正方形的边长为:
=
.
否则,由于y=x3+ax为奇函数,因此A、B、C、D关于O点的对称点A′、B′、C′、D′也在曲线上,
且A′B′C′D′也是正方形,与题设矛盾.设四点为A(x0,y0),B(-y0,x0),C(-x0,-y0),D(y0,-x0),其中x0>0,y0>0,
则y0=x03+ax0,①,-x0=y03+ay0,②,
①×x0+②×y0,得:x04+y04+a(x02+y02)=0,③
①×y0-②×x0,得:x02+y02=x0y0(x02-y02),④
令x0=rcosθ,y0=rsinθ,r>0,θ∈(0,
| π |
| 2 |
由③④得:a=-r2(1-2sin2θcos2θ)
消去r2,得关于sin2θ的方程:
(1+a2)(sin22θ)2-(4+a2)sin22θ+4=0
因sin22θ在(0,1)内只有一个根,
∴△=(a2+4)2-16(1+a2)=a4-8a2=0,
∴a=-2
| 2 |
| ||
| 2 |
2
| ||
| 3 |
| 18 |
∴正方形的边长为:
| 2r |
| 4 | 72 |
点评:本题考查了三角函数问题,考查了二次函数的性质,考查转化思想,是一道中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
如图,正四面体ABCD的棱长为2,点E,F分别为棱BC,AD的中点,则
•
的值为( )
| EF |
| BA |

| A、4 | B、-4 | C、-2 | D、2 |
若f(x)是定义在R上的增函数,则对任意x、y∈R,“f(x)+f(y)<f(-x)+f(-y)”是“x+y<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
sin(-660°)=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
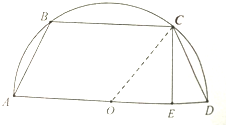 在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.
在半径为1的半圆中,作如图所示的等腰梯形ABCD,CE垂直下底AD于E,设DE=x(0<x<1),CE=h,梯形ABCD的周长为L.