题目内容
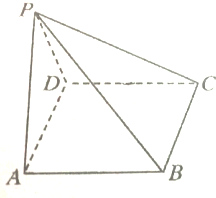如图所示，在四棱锥P-ABCD中，底面ABCD是矩形，且PA⊥平面ABCD，PA=5，AB=4，AD=3，求直线PC与平面ABCD所成的角．考点：直线与平面所成的角
专题：计算题,空间位置关系与距离,空间角
分析：连接AC，由于PA⊥平面ABCD，则∠PCA即为直线PC与平面ABCD所成的角，通过解直角三角形PAC，即可得到所求值．
解答：
解：连接AC，由于PA⊥平面ABCD，
则∠PCA即为直线PC与平面ABCD所成的角，
在矩形ABCD中，AB=4，BC=3，则AC=
=5．
在直角△PAC中，PA=AC=5，则∠PCA=45°，
则有直线PC与平面ABCD所成的角为45°．
解：连接AC，由于PA⊥平面ABCD，则∠PCA即为直线PC与平面ABCD所成的角，
在矩形ABCD中，AB=4，BC=3，则AC=
| 32+42 |
在直角△PAC中，PA=AC=5，则∠PCA=45°，
则有直线PC与平面ABCD所成的角为45°．
点评：本题考查空间直线和平面所成的角的求法，考查运算能力，属于基础题．
练习册系列答案
相关题目
如果复数z=i（-1+i），则（ ）
| A、|z|=2 |
| B、z的实部为1 |
| C、z的共轭复数为1+i |
| D、z的虚部为-1 |
已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为10、高为5的等腰三角形，侧视图（或称左视图）是一个底边长为8、高为5的等腰三角形，求该几何体的表面积S．已知函数f（x）=
则方程f（x）=1解的个数为（ ）
|
| A、1 | B、2 | C、3 | D、4 |