题目内容
已知函数f(x)=ln(1+x)-
x2在区间[0,2)上最大值是 .
| 1 |
| 4 |
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:由题意求导f′(x)=
-
x=-
,利用导数的正负确定函数的单调性,从而求最大值.
| 1 |
| 1+x |
| 1 |
| 2 |
| (x-1)(x+2) |
| 2(1+x) |
解答:
解:∵f′(x)=
-
x=-
,
∴函数f(x)=ln(1+x)-
x2在[0,1]上单调递增,在[1,2)上单调递减,
∴函数f(x)=ln(1+x)-
x2在区间[0,2)上最大值为
f(1)=ln2-
.
故答案为:ln2-
.
| 1 |
| 1+x |
| 1 |
| 2 |
| (x-1)(x+2) |
| 2(1+x) |
∴函数f(x)=ln(1+x)-
| 1 |
| 4 |
∴函数f(x)=ln(1+x)-
| 1 |
| 4 |
f(1)=ln2-
| 1 |
| 4 |
故答案为:ln2-
| 1 |
| 4 |
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则f[f(
)]的值是( )
|
| 1 |
| 2 |
| A、3 | ||
B、
| ||
C、log2
| ||
| D、0 |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.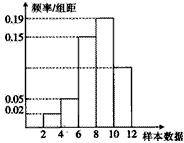 有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为
有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为