题目内容
15.若f(x)是定义在(0,+∞)的函数,且f(x)>0.满足2f(x)+xf′(x)>0,则下列不等式正确的是( )| A. | 2016f(2016)>2015f(2015) | B. | 2016f(2016)<2015f(2015) | ||
| C. | 20152f(2015)<20162f(2016) | D. | 20152f(2015)>20162f(2016) |
分析 构造函数g(x)=x2f(x),求出函数的导数,利用函数的单调性判断选项即可.
解答 解:构造函数g(x)=x2f(x),g'(x)=2xf(x)+x2f'(x)>0,
所以g(x)在(0,+∞)单调递增,
所以20152f(2015)<20162f(2016),结合不等式性质.
故选:C.
点评 本题考查函数的单调性的应用,构造法的应用,考查转化思想以及计算能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
10.梯形ABCD中,$\overrightarrow{AB}$=λ$\overrightarrow{AD}$+μ$\overrightarrow{BC}$,则λ+μ=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 不能确定 |
7.在四面体ABCD中,已知棱AC的长为$\sqrt{3}$,其余各棱长都为2,则二面角A-BD-C的大小为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
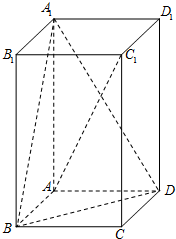 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.