题目内容
7.在四面体ABCD中,已知棱AC的长为$\sqrt{3}$,其余各棱长都为2,则二面角A-BD-C的大小为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 取BD的中点E,连接AE、CE,证明∠AEC就是A-BD-C的二面角,解三角形ACE即可得到二面角A-BD-C的大小.
解答  解:取BD的中点E,连接AE、CE
解:取BD的中点E,连接AE、CE
∵AB=AD=BC=CD,
∴CE⊥BD,AE⊥BD
∴∠AEC就是A-BD-C的二面角
∵AB=AD=BD=BC=CD=2,∴AE=CE=$\sqrt{3}$,又因为AC=$\sqrt{3}$,∴∠AEC=$\frac{π}{3}$.
即二面角A-BD-C的大小为$\frac{π}{3}$.
故选:B.
点评 本题考查二面角的平面角及求法,其中构造出二面角A-BD-C的平面角∠AEC是解答本题的关键,属于基础题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15.若f(x)是定义在(0,+∞)的函数,且f(x)>0.满足2f(x)+xf′(x)>0,则下列不等式正确的是( )
| A. | 2016f(2016)>2015f(2015) | B. | 2016f(2016)<2015f(2015) | ||
| C. | 20152f(2015)<20162f(2016) | D. | 20152f(2015)>20162f(2016) |
16.对于R上可导的任意函数f(x),若满足f(x)=f(2-x),且(x-1)f′(x)≥0,则必有( )
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
17.函数$f(x)=sinx-\frac{1}{2}x(x∈(-π,π)$的极大值点为( )
| A. | $(\frac{π}{3},\frac{{\sqrt{3}}}{2}-\frac{π}{6})$ | B. | $(-\frac{π}{3},\frac{π}{6}-\frac{{\sqrt{3}}}{2})$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
 的图象大致是( )
的图象大致是( )
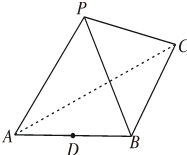 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.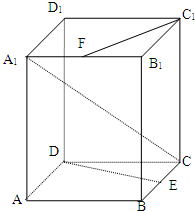 已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点.
已知棱长为a的正方体ABCD-A1B1C1D1中,E是BC的中点,F为A1B1的中点.