题目内容
6.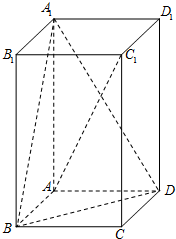 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.(1)若h=2,求AC1与平面A1BD所成角的正弦值;
(2)若二面角A1-BD-C的大小为$\frac{3}{4}$π,求h的值.
分析 (1)以点A为坐标原点,AB,AD,AA1分别为x,y,z轴,建立空间直角坐标系O-xyz,利用向量法能求出AC1与平面A1BD所成角的正弦值.
(2)求出平面A1BD的法向量和平面CBD的法向量,利用向量法能求出结果.
解答 解:(1)如图,以点A为坐标原点,AB,AD,AA1分别为x,y,z轴,建立空间直角坐标系O-xyz,
当h=2时,B(1,0,0),D(0,1,0),A1(0,0,2),C1(1,1,2),
则$\overrightarrow{A{C_1}}=(1,1,2)$,$\overrightarrow{{A_1}B}=(1,0,-2)$,$\overrightarrow{{A_1}D}=(0,1,-2)$,
设平面A1BD的法向量$\overrightarrow{n}$=(a,b,c),
则由$\left\{\begin{array}{l}{\overrightarrow{{A}_{1}B}•\overrightarrow{n}=a-2c=0}\\{\overrightarrow{{A}_{1}D}•\overrightarrow{n}=b-2c=0}\end{array}\right.$,
不妨取c=1,则a=b=2,此时$\overrightarrow{n}$=(2,2,1),
故cos<$\overrightarrow{A{C}_{1}},\overrightarrow{n}$>=$\frac{\overrightarrow{A{C}_{1}}•\overrightarrow{n}}{|\overrightarrow{A{C}_{1}}|•|\overrightarrow{n}|}$=$\frac{\sqrt{6}}{3}$,
设AC1与平面A1BD所成角为θ,
则sinθ=$\sqrt{1-(\frac{\sqrt{6}}{3})^{2}}$=$\frac{\sqrt{3}}{3}$.
所以AC1与平面A1BD所成角的正弦值为$\frac{{\sqrt{3}}}{3}$;(5分)
(2)由A1(0,0,h)得,$\overrightarrow{{A_1}B}=(1,0,-h)$,$\overrightarrow{{A_1}D}=(0,1,-h)$,
设平面A1BD的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{A}_{1}B}=x-hz=0}\\{\overrightarrow{m}•\overrightarrow{{A}_{1}D}=y-hz=0}\end{array}\right.$,
不妨取z=1,则x=y=h,此时$\overrightarrow{m}$=(h,h,1),(7分)
又平面CBD的法向量$\overrightarrow{A{A_1}}=(0,0,h)$,
故$cos<\overrightarrow{A{A}_{1}},\overrightarrow{m}>$=$\frac{\overrightarrow{A{A}_{1}}•\overrightarrow{m}}{|\overrightarrow{A{A}_{1}}|•|\overrightarrow{m}|}$=$\frac{h}{\sqrt{1+2{h}^{2}}•h}$=$\frac{\sqrt{2}}{2}$,
解得$h=\frac{{\sqrt{2}}}{2}$.(10分)
点评 本题考查线面角的正弦值的求法,考查线的涂布以的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 同步轻松练习系列答案
同步轻松练习系列答案| A. | (-3,0) | B. | (3,0) | C. | (-1,3) | D. | (-2,0) |
| A. | y=sinx | B. | y=log2|x| | C. | y=x2-$\frac{1}{2}$ | D. | y=$\frac{1}{x}$ |
| A. | 2016f(2016)>2015f(2015) | B. | 2016f(2016)<2015f(2015) | ||
| C. | 20152f(2015)<20162f(2016) | D. | 20152f(2015)>20162f(2016) |
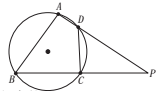 如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P.
如图,已知圆内接四边形ABCD中,AB=BC,AD的延长线与BC的延长线交于点P. 的图象大致是( )
的图象大致是( )