题目内容
4.设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z),若f(2009)=5,则f(2015)等于( )| A. | 4 | B. | 3 | C. | -5 | D. | 5 |
分析 利用诱导公式求得 asinα+bcosβ=-1,由此利用诱导公式求得f(2015)的值.
解答 解:f(x)=asin(πx+α)+bcos(πx+β)+4,其中a,b,α,β∈R,且ab≠0,α≠kπ(k∈Z),
若f(2009)=asin(2009π+α)+bcos(2009π+β)+4=-asinα-bcosβ+4=5,
∴asinα+bcosβ=-1,则f(2015)=asin(2015π+α)+bcos(2015π+β)+4=-asinα-bcosβ+4=5,
故选:D.
点评 本题主要考查诱导公式的应用,求三角函数的值,属于基础题.

练习册系列答案
相关题目
15.若f(x)是定义在(0,+∞)的函数,且f(x)>0.满足2f(x)+xf′(x)>0,则下列不等式正确的是( )
| A. | 2016f(2016)>2015f(2015) | B. | 2016f(2016)<2015f(2015) | ||
| C. | 20152f(2015)<20162f(2016) | D. | 20152f(2015)>20162f(2016) |
19.已知函数f(x)=xα,当x∈(1,+∞)时,f(x)-x<0,则( )
| A. | 0<α<1 | B. | α<1 | C. | α>0 | D. | α<0 |
16.对于R上可导的任意函数f(x),若满足f(x)=f(2-x),且(x-1)f′(x)≥0,则必有( )
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
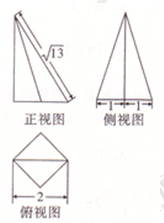 一个四棱锥的底面为正方形,其三视图如图所示,根据图中标出的尺寸(单位:cm),则这个四棱锥的外接球的表面积是13π.
一个四棱锥的底面为正方形,其三视图如图所示,根据图中标出的尺寸(单位:cm),则这个四棱锥的外接球的表面积是13π. 为偶函数,且在
为偶函数,且在 单调递增,则
单调递增,则 的解集为( )
的解集为( ) 或
或 B.
B.
 或
或 D.
D.
 的图象大致是( )
的图象大致是( )