题目内容
3.已知函数f(x)=$\frac{x}{k}$-lnx(k>0)(1)求f(x)的最小值;
(2)若k=2,判断方程f(x)-1=0在区间($\frac{1}{e}$,1)内实数解的个数;
(3)证明:对任意给定的M>0,总存在正数x0,使得当x>x0时,恒有$\frac{x}{2}$-M>lnx.
分析 (1)先求出导函数,再根据函数的单调性即可求出函数的最小值,
(2)根据函数的零点定理,即可判断方程f(x)-1=0在区间($\frac{1}{e}$,1)内实数解的个数,
(3)根据(1)的结论,得到$\frac{x}{3}-1+ln3≥lnx$①,$\frac{x}{2}-M>\frac{x}{3}-1+ln3$②,即可证明结论.
解答 解:(1)$f'(x)=\frac{1}{k}-\frac{1}{x}=\frac{x-k}{kx}$
当0<x<k时,f'(x)<0,当x>k时,f'(x)>0,
所以f(x)在(0,k)单调递减,在(k,+∞)单调递增,
从而f(x)min=f(k)=1-lnk,
(2)k=2时,$f(x)-1=\frac{x}{2}-lnx-1$
因为$f(\frac{1}{e})-1=\frac{1}{2e}>0$,$f(1)-1=-\frac{1}{2}<0$,且f(x)的图象是连续的,
所以f(x)-1=0在区间$(\frac{1}{e},1)$内有实数解;
又当$x∈(\frac{1}{e},1)$时,$f'(x)=\frac{x-2}{2x}<0$,所以f(x)在(0,1)上单调递减,
从而f(x)-1=0在区间$({\frac{1}{e},1})$内至多有一个实数解,
故f(x)-1=0在区间$({\frac{1}{e},1})$内有唯一的有实数解.
(3)证明:由(1)知:${(\frac{x}{3}-lnx)_{min}}=1-ln3$
所以x>0时,$\frac{x}{3}-1+ln3≥lnx$①
由$\frac{x}{2}-M>\frac{x}{3}-1+ln3$得:x>6(M-1+ln3)
所以x>6(M-1+ln3)>0时,$\frac{x}{2}-M>\frac{x}{3}-1+ln3$②
由①②知:取x0=6(M-1+ln3)>0,则当x>x0时,
有$\frac{x}{2}-M>\frac{x}{3}-1+ln3≥lnx$,
即$\frac{x}{2}-M>lnx$成立.
点评 本题考查了导数的应用问题,也考查运算求解能力以及逻辑推理能力,考查了函数与方程思想的应用问题,是难题目.

 名校课堂系列答案
名校课堂系列答案| A. | {x>-2011} | B. | {x|x<-2011} | C. | {x|-2011<x<0} | D. | {x|-2016<x<-2011} |
| A. | 2016f(2016)>2015f(2015) | B. | 2016f(2016)<2015f(2015) | ||
| C. | 20152f(2015)<20162f(2016) | D. | 20152f(2015)>20162f(2016) |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC的中点.△PAD是边长为2的正三角形,BC=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC的中点.△PAD是边长为2的正三角形,BC=1,CD=$\sqrt{3}$.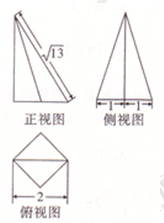 一个四棱锥的底面为正方形,其三视图如图所示,根据图中标出的尺寸(单位:cm),则这个四棱锥的外接球的表面积是13π.
一个四棱锥的底面为正方形,其三视图如图所示,根据图中标出的尺寸(单位:cm),则这个四棱锥的外接球的表面积是13π.