题目内容
20．已知过点P（0，2）的直线l与圆（x-1）2+y2=5相切，且与直线ax-2y+1=0垂直，则a=（ ）| A． | 2 | B． | 4 | C． | -4 | D． | 1 |
分析 由题意判断点在圆上，求出P与圆心连线的斜率就是直线ax-2y+1=0的斜率，然后求出a的值即可．
解答 解：因为点P（0，2）满足圆（x-1）2+y2=5的方程，所以P在圆上，
又过点P（0，2）的直线与圆（x-1）2+y2=5相切，且与直线ax-2y+1=0垂直，
所以切点与圆心连线与直线ax-2y+1=0平行，
所以直线ax-2y+1=0的斜率为：$\frac{a}{2}=\frac{2-0}{0-1}$，
所以a=-4．
故选：C．
点评 本题考查直线与圆的位置关系，直线与直线的垂直，考查转化思想与计算能力．
练习册系列答案
考前必练系列答案
相关题目
11．某学校课题组为了研究学生的数学成绩和物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（百分制）如表所示：
若数学成绩90分（含90分）以上为优秀，物理成绩85（含85分）以上为优秀．有多少把握认为学生的学生成绩与物理成绩有关系（ ）
参考数据公式：①独立性检验临界值表
②独立性检验随机变量K2的值的计算公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$．
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
参考数据公式：①独立性检验临界值表
| P（K2≥k0） | 0.50 | 0.40 | 0.25 | 015． | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6356． | 7.879 | 10.828 |
| A． | 99.9% | B． | 99.5% | C． | 97.5% | D． | 95% |
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，AD⊥DC，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC的中点．△PAD是边长为2的正三角形，BC=1，CD=$\sqrt{3}$．
15．若f（x）是定义在（0，+∞）的函数，且f（x）＞0．满足2f（x）+xf′（x）＞0，则下列不等式正确的是（ ）
| A． | 2016f（2016）＞2015f（2015） | B． | 2016f（2016）＜2015f（2015） | ||
| C． | 20152f（2015）＜20162f（2016） | D． | 20152f（2015）＞20162f（2016） |
5．过原点且倾斜角为60°的直线被圆x2+y2-4x=0所截得的弦长为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{6}$ | D． | $2\sqrt{3}$ |
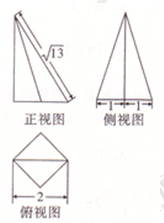一个四棱锥的底面为正方形，其三视图如图所示，根据图中标出的尺寸（单位：cm），则这个四棱锥的外接球的表面积是13π．
为偶函数，且在
单调递增，则
的解集为（ ）
或
B．
或
D．