题目内容
10.函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(-t)+4034t+2017,则实数t的取值范围是( )| A. | $({-\frac{1}{2},+∞})$ | B. | $({-\frac{3}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{3}{2}})$ |
分析 构造函数g(x)=f(x)-2017x2+2017x,根据函数的单调性得到g(t+1)<g(-t),得到关于t的不等式,求出t的范围即可.
解答 解:设g(x)=f(x)-2017x2+2017x,
则g′(x)=f′(x)-4034x+2017<0,
故g(x)在R递减,
而g(t+1)-g(-t)=f(t+1)-f(-t)-4034t-2017<0,
即g(t+1)<g(-t),
故t+1>-t,解得:t>-$\frac{1}{2}$,
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的表面积为( )
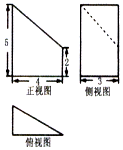

| A. | 45 | B. | $45+\frac{{9\sqrt{2}}}{2}$ | C. | $\frac{117}{2}$ | D. | 60 |
19.已知平面向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a•({\overrightarrow a+\overrightarrow b})=3$,且$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,则向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
