题目内容

3．函数$f（x）={e^{x^2}}-2{x^2}$的图象大致为（　　）
A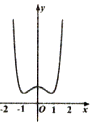．B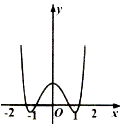．C．D．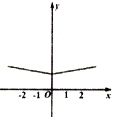

分析 求出函数的导数，求出极值点以及函数的极值的符号，判断选项即可．

解答 解：函数$f（x）={e^{x^2}}-2{x^2}$，可得f′（x）=2x（${e}^{{x}^{2}}-2$），令f′（x）=0，可得x=0或x=$±\sqrt{ln2}$，
函数由3个极值点，排除C，D；
当x=$\sqrt{ln2}$时，f（$\sqrt{ln2}$）=2（1-ln2）＞0，排除B，
故选：A．

点评 本题考查函数的导数的应用，函数的极值点的求法，函数的图象的判断，是中档题．

练习册系列答案
相关题目
13．函数$y=\frac{1}{3}{x^3}+b{x^2}+（b+2）x+3$在R上不是单调增函数则b范围为（　　）
A．（-1，2）B．（-∞，-1]∪[2，+∞）C．[-1，2]D．（-∞，-1）∪（2，+∞）
14．设抛物线y2=4x的焦点为F，过点F作直线l与抛物线分别交于两点A，B，若点M满足$\overrightarrow{OM}$=$\frac{1}{2}$（$\overrightarrow{OA}$+$\overrightarrow{OB}$），过M作y轴的垂线与抛物线交于点P，若|PF|=2，则M点的横坐标为3．
11．设椭圆$\frac{x^2}{2}+{y^2}=1$的左、右焦点分别为F1、F2，点P在该椭圆上，则使得△F1F2P是等腰三角形的点P的个数是6．
18．设a∈R，函数$f（x）=\frac{{{2^x}+a}}{{{2^x}+1}}$；
（1）求a的值，使得f（x）为奇函数；
（2）若$f（x）＜\frac{a+2}{2}$对任意x∈R成立，求a的取值范围．
8．以下四个命题中，正确命题的个数是（　　）
①命题“若x=y，则sinx=siny”的逆否命题是真命题；
②已知α，β是不同的平面，m，n是不同的直线，m∥α，n∥β，α⊥β，则m⊥n；
③直线l1：2ax+y+1=0，l2：x+2ay+2=0，l1∥l2的充要条件是$a=\frac{1}{2}$；
④$\int_{-1}^1{sinxdx=0}$．
A．1B．2C．3D．4
15．设函数$f（x）=4lnx-\frac{1}{2}a{x^2}+（{4-a}）x（{a∈R}）$．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若函数f（x）存在极值，对于任意的0＜x1＜x2，存在正实数x0，使得f（x1）-f（x2）=f'（x0）•（x1-x2），试判断x1+x2与2x0的大小关系并给出证明．
12．若x＞y＞1，0＜a＜b＜1，则下列各式中一定成立的是（　　）
A．xa＞ybB．xa＜ybC．ax＜byD．ax＞by
13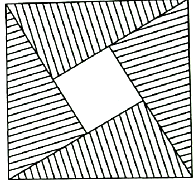．如图所示，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形的概率为$\frac{1}{5}$，设直角三角形中较大的锐角为θ，则sinθ=（　　）
A．$\frac{{\sqrt{5}}}{5}$B．$\frac{{2\sqrt{5}}}{5}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{{\sqrt{2}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网