题目内容
三棱椎的三视图为如图所示的三个直角三角形，则三棱锥的表面积为（ ）
A、4+4
| ||||
B、2+2
| ||||
C、
| ||||
D、2+2
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体为三棱锥，根据三视图判断几何体的结构特征，并结合直观图判断相关几何量的数据，把数据代入棱锥的表面积公式计算．
解答：
解：由三视图知：几何体为三棱锥，如图：
其中SA⊥平面ABC，AB⊥BC，SA=BC=2，AB=1，AC=
，SB=
，
BC⊥平面SAB，SB?平面SAB，∴SB⊥BC，
∴几何体的表面积S=2×
×2×1+2×
×2×
=2+2
．
故选：B．
其中SA⊥平面ABC，AB⊥BC，SA=BC=2，AB=1，AC=
| 5 |
| 5 |
BC⊥平面SAB，SB?平面SAB，∴SB⊥BC，
∴几何体的表面积S=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
故选：B．
点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的结构特征是解题的关键．
练习册系列答案
相关题目
甲、乙、丙三人射击击中目标的概率分别为
，
，
．现在三人同时射击目标，则目标被击中的概率为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在平面直角坐标系中，不等式组
（a为常数）所表示的平面区域的面积是9，则实数a的值是（ ）
|
| A、1 | B、-5 |
| C、1或-5 | D、-1或5 |
已知双曲线
-
=1的焦点到一条渐近线的距离为1，则该双曲线的离心率为（ ）
| x2 |
| 3 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
曲线
+
=1的焦点坐标为（ ）
| y2 |
| 16 |
| x2 |
| 9 |
A、（0，±
| ||
B、（±
| ||
| C、（0，±5） | ||
| D、（±5，0） |
设某种产品分两道工序生产，第一道工序的次品率为10%，第二道工序的次品率为3%．生产这种产品只要有一道工序出次品就出次品，则该产品的次品率是（ ）
| A、0.13 | B、0.03 |
| C、0.127 | D、0.873 |
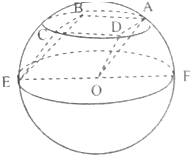如图，三棱柱OAD-EBC，其中A，B，C，D，E均在以O为球心，半径为2的球面上，EF为直径，侧面ABCD为边长等于2的正方形，则三棱柱OAD-EBC的体积为（ ）