题目内容
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
| D、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.可举反例,比如f(x)=x3,f′(x)=3x2,f′(0)=0,但x=0不是极值点,即可判断;
B.由含有一个量词的命题的否定形式,即可判断;
C.根据偶函数的定义,结合充分必要条件的定义,即可判断;
D.在三角形ABC中,运用正弦定理,结合四种命题和相互关系,即可判断.
B.由含有一个量词的命题的否定形式,即可判断;
C.根据偶函数的定义,结合充分必要条件的定义,即可判断;
D.在三角形ABC中,运用正弦定理,结合四种命题和相互关系,即可判断.
解答:
解:A.函数y=f(x)为R上的可导函数,则x0为函数f(x)极值点可推出f′(x0)=0,反之不成立,
比如f(x)=x3,f′(x)=3x2,f′(0)=0,但x=0不是极值点,故A错;
B.命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,故B错;
C.“b=0”可推出“函数f(x)=ax2+bx+c是偶函数”,反之,则f(-x)=f(x),可推出b=0,故C正确;
D.在△ABC中,若A>B?a>b?2RsinA>2RsinB,即sinA>sinB,故其逆命题也为真命题,即D错.
故选:C.
比如f(x)=x3,f′(x)=3x2,f′(0)=0,但x=0不是极值点,故A错;
B.命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,故B错;
C.“b=0”可推出“函数f(x)=ax2+bx+c是偶函数”,反之,则f(-x)=f(x),可推出b=0,故C正确;
D.在△ABC中,若A>B?a>b?2RsinA>2RsinB,即sinA>sinB,故其逆命题也为真命题,即D错.
故选:C.
点评:本题以命题的真假判断为载体考查四种命题及真假、充分必要条件的判断、命题的否定,同时考查函数的极值点、函数的奇偶性、解三角形的正弦定理,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知命题p:?x∈R,cosx≥a,下列的取值能使“¬p”命题是真命题的是( )
| A、a∈R | B、a=2 |
| C、a=1 | D、a=0 |
对于函数f(x),若存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[λm,λn],则称f(x)为“λ倍函数”,若f(x)=ax(a>1)为“1倍函数”,则a的取值范围为( )
A、(1,
| ||
B、(
| ||
C、(1,e
| ||
D、(e
|
已知点F1,F2分别是椭圆
+
=1(a>b>0)的左、右焦点,点P是椭圆上的一个动点,若使得满足△PF1F2是直角三角形的动点P恰好有6个,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=|x+2|-|x-1|,则f(x)的值域是( )
| A、(-3,3) |
| B、[-3,3] |
| C、[3,+∞) |
| D、[-3,+∞) |
已知p:|x-2|<3,q:0<x<5,那么p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
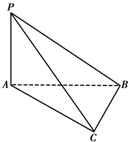 如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )
如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )| A、一对 | B、两对 | C、三对 | D、四对 |
下列关于独立性检验的说法中,错误的是( )
| A、独立性检验得到的结论一定正确 |
| B、独立性检验依赖小概率原理 |
| C、样本不同,独立性检验的结论可能有差异 |
| D、独立性检验不是判定两事物是否相关的唯一方法 |