题目内容
已知命题p:?x∈R,cosx≥a,下列的取值能使“¬p”命题是真命题的是( )
| A、a∈R | B、a=2 |
| C、a=1 | D、a=0 |
考点:命题的否定
专题:概率与统计
分析:写出命题的否定形式,然后判断选项即可.
解答:
解:命题p:?x∈R,cosx≥a,则¬p,?x∈R,cosx<a,
能使“¬p”命题是真命题,由余弦函数的值域可知,cosx≤1,
故选项C成立.
故选:C.
能使“¬p”命题是真命题,由余弦函数的值域可知,cosx≤1,
故选项C成立.
故选:C.
点评:本题考查特称命题的真假的判断与应用,三角函数的值域的应用,基本知识的考查.

练习册系列答案
相关题目
若α,β∈(0,
),sin(α-
)=
,sin(
-β)=-
,则cos(α+β)的值等于( )
| π |
| 2 |
| β |
| 2 |
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
命题“若p则q”的逆否命题是( )
| A、若q则p |
| B、若¬p则¬q |
| C、若¬q则¬p |
| D、若p则¬q |
函数f(x)=x3+x在实数范围内( )
| A、单调递增 | B、单调递减 |
| C、先增后减 | D、先减后增 |
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
| D、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
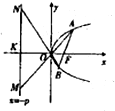 如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则