题目内容
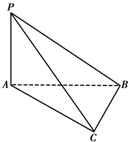 如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )
如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )| A、一对 | B、两对 | C、三对 | D、四对 |
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:由PA垂直于△ABC所在平面,得到平面PAB⊥平面ABC,平面PAC⊥平面ABC,由线面垂直得PA⊥BC,又∠ACB=90°,所以BC⊥平面PAC,由此得平面PBC⊥平面PAC,故图形中互相垂直的平面有3对.
解答:
 解:∵PA垂直于△ABC所在平面,连结PB、PC,
解:∵PA垂直于△ABC所在平面,连结PB、PC,
∵PA?平面PAB,∴平面PAB⊥平面ABC,
又∵PA?平面PAC,∴平面PAC⊥平面ABC,
∵PA垂直于△ABC所在平面,
∴PA⊥BC,又∠ACB=90°,∴BC⊥AC,
∴BC⊥平面PAC,
∵BC?平面PBC,
∴平面PBC⊥平面PAC.
∴图形中互相垂直的平面有3对.
故选:C.
 解:∵PA垂直于△ABC所在平面,连结PB、PC,
解:∵PA垂直于△ABC所在平面,连结PB、PC,∵PA?平面PAB,∴平面PAB⊥平面ABC,
又∵PA?平面PAC,∴平面PAC⊥平面ABC,
∵PA垂直于△ABC所在平面,
∴PA⊥BC,又∠ACB=90°,∴BC⊥AC,
∴BC⊥平面PAC,
∵BC?平面PBC,
∴平面PBC⊥平面PAC.
∴图形中互相垂直的平面有3对.
故选:C.
点评:本题考查平面与平面垂直的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
| D、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
令P(x):ax2+3x+2>0,若对任意x∈R,P(x)是真命题,则实数a的取值范围是( )
| A、a>0 | ||
B、a>
| ||
| C、a<0 | ||
| D、a=0 |
将编号为1,2,3,4,5,6的六个小球排成一列,要求1号球与2号球必须相邻,4号球、5号球、6号球互不相邻,则不同的排法种数有( )
| A、4 | B、24 | C、72 | D、144 |
已知m,n是不同的直线,α,β是不重合的平面,下列命题正确的是( ):
| A、若m∥α,则m平行于平面α内的任意一条直线 |
| B、若α∥β,m?α,n?β,则m∥n |
| C、若α∥β,m?α,则m∥β. |
| D、若m?α,n?α,m∥β,n∥β,则α∥β |
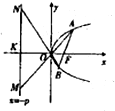 如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
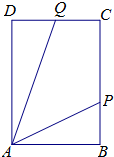 如图,ABCD是长方形海域,其中AB=10海里,AD=10
如图,ABCD是长方形海域,其中AB=10海里,AD=10