题目内容
对于函数f(x),若存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[λm,λn],则称f(x)为“λ倍函数”,若f(x)=ax(a>1)为“1倍函数”,则a的取值范围为( )
A、(1,
| ||
B、(
| ||
C、(1,e
| ||
D、(e
|
考点:函数的值域
专题:函数的性质及应用
分析:先根据函数的定义判断出方程ax=x,有两个不同实数解,进而分别设出f(x)=ax,g(x)=x,分别进行求导,通过极值的对比建立不等式求得a的范围.
解答:
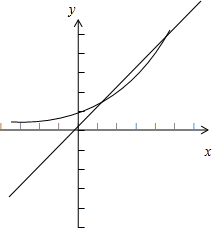 解:∵f(x)=ax(a>1)为“1倍函数”,
解:∵f(x)=ax(a>1)为“1倍函数”,
∴f(x)在区间[m,n]上的值域为[m,n],
∵a>1,
∴f(x)为增函数,
∴
,
即方程ax=x,有两个不同实数解,
设f(x)=ax,g(x)=x,
则f′(x)=axlna,g′(x)=1,
令f′(x0)=g′(x0),即ax0lna=1,
∴a x0=
=logae,x0=loga(logae),
如图可知g(x0)>f(x0),
∴x0>a x0,即loga(logae)>logae,
∵a>1,
∴logae>e>0,
∴0<logea<
,
∴1<a<e
,
故选:C.
 解:∵f(x)=ax(a>1)为“1倍函数”,
解:∵f(x)=ax(a>1)为“1倍函数”,∴f(x)在区间[m,n]上的值域为[m,n],
∵a>1,
∴f(x)为增函数,
∴
|
即方程ax=x,有两个不同实数解,
设f(x)=ax,g(x)=x,
则f′(x)=axlna,g′(x)=1,
令f′(x0)=g′(x0),即ax0lna=1,
∴a x0=
| 1 |
| lna |
如图可知g(x0)>f(x0),
∴x0>a x0,即loga(logae)>logae,
∵a>1,
∴logae>e>0,
∴0<logea<
| 1 |
| e |
∴1<a<e
| 1 |
| e |
故选:C.
点评:本题主要考查了函数的性质,导数的性质与应用.考查了学生分析能力,数形结合思想起到了重要作用.

练习册系列答案
相关题目
函数f(x)=x3+x在实数范围内( )
| A、单调递增 | B、单调递减 |
| C、先增后减 | D、先减后增 |
双曲线5x2+ky2=5的一个焦点是(
,0),那么实数k的值为( )
| 6 |
| A、-25 | B、25 | C、-1 | D、1 |
已知p:
≤1,q:(x-a)(x-a-1)≤0,若p是q的充分而不必要条件,则实数a的取值范围为( )
| 2x-1 |
A、(-∞,0)∪(
| ||
B、(-∞,0]∪[
| ||
C、[0,
| ||
D、(0,
|
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
| D、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
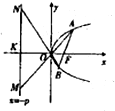 如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则