题目内容
20.当α∈($\frac{π}{2}$,$\frac{3π}{4}$)时,方程x2sinα-y2cosα=1表示的曲线是( )| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
分析 判断三角函数的符号、范围,即可判断曲线的形状.
解答 解:α∈($\frac{π}{2}$,$\frac{3π}{4}$)时,sinα∈($\frac{\sqrt{2}}{2}$,1),cosα∈(-$\frac{\sqrt{2}}{2}$,0),
可得方程x2sinα-y2cosα=1表示的曲线是焦点在y轴上的椭圆.
故选:B.
点评 本题考查椭圆的简单性质的应用,三角函数符号的判断,考查计算能力.

练习册系列答案
相关题目
8.设P={x|x<1},Q={x|x2<1},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
15.已知抛物线的标准方程为x2=8y,则抛物线的准线方程为( )
| A. | x=2 | B. | x=-2 | C. | y=2 | D. | y=-2 |
5.若等比数列{an}的前n项和Sn满足Sn=a-($\frac{1}{2}$)n-1,则直线(a-1)x-y+3=0与圆(x-a)2+y2=12的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
9.已知三棱锥S-ABC,其三视图中的正(主)视图和侧(左)视图如图所示,则该三棱锥的体积为( )
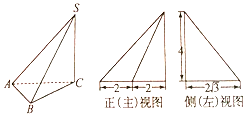

| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $16\sqrt{3}$ |
10.已知等差数列{an}的前n项和为Sn,若$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$,则$\frac{{S}_{9}}{{S}_{5}}$=( )
| A. | $\frac{9}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |