题目内容
19.若直线x-2y+m=0与圆x2+y2-4x+6y+8=0相切,则实数m=-3或-13.分析 利用直线x-2y+m=0与圆x2+y2-4x+6y+8=0相切,圆心到直线的距离等于半径,即可求出m的值.
解答 解:圆x2+y2-4x+6y+8=0的圆心坐标为(2,-3),半径为$\sqrt{5}$
因为直线x-2y+m=0与圆x2+y2-4x+6y+8=0相切,
所以圆心到直线的距离$\frac{|2+6+m|}{\sqrt{5}}$=$\sqrt{5}$,所以m=-3或-13.
故答案为:-3或-13.
点评 本题考查直线与圆的位置关系的应用,考查计算能力,比较基础.

练习册系列答案
相关题目
9.已知三棱锥S-ABC,其三视图中的正(主)视图和侧(左)视图如图所示,则该三棱锥的体积为( )
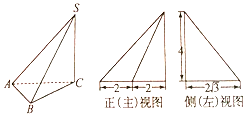

| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $16\sqrt{3}$ |
10.已知等差数列{an}的前n项和为Sn,若$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$,则$\frac{{S}_{9}}{{S}_{5}}$=( )
| A. | $\frac{9}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |
4.数列-1,3,-5,7,-9,…的一个通项公式为( )
| A. | an=2n-1 | B. | an=(-1)n(1-2n) | C. | an=(-1)n(2n-1) | D. | an(-1)n+1(2n-1) |
11.为了在运行如图的程序之后输出的值为5,则输入x的所有可能的值是( )


| A. | 5 | B. | -5 | C. | 5或0 | D. | -5或5 |
8.某四棱锥的三视图如图所示,则俯视图的面积为( )
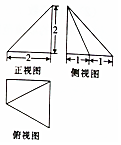

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
9.已知tan($\frac{π}{4}$+α)=$\frac{1}{2}$,则tanα的值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -1 |
