某市教育局随机调查了300名高中学生周末的学习时间.制成了如图所示的频率分布直方图.其中学习时间的范围是[0.30].样本数据分组为.[0.5).[5.10).[10.15).[15.20).[20.25).[25.30].根据直方图.这300名高中生周末的学习时间不少于15小时的人数是( )A．27B．33C．135D．165 题目和参考答案——青夏教育精英家教网——

题目内容

1．

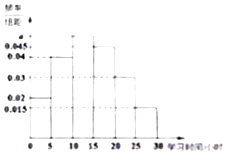某市教育局随机调查了300名高中学生周末的学习时间（单位：小时），制成了如图所示的频率分布直方图，其中学习时间的范围是[0，30]，样本数据分组为，[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]，根据直方图，这300名高中生周末的学习时间不少于15小时的人数是（　　）

A．

27

B．

33

C．

135

D．

165

分析先由频率分布直方图计算出学习时间不少于15小时的频率，进而可得学习时间不少于15小时的人数．

解答解：学习时间不少于15小时的频率为（0.045+0.03+0.015）×5=0.45，
故这300名高中生周末的学习时间不少于15小时的人数是300×0.45=135，
故选：C

点评本题考查的知识点是频率分布直方图，频数计算，难度不大，属于基础题．

练习册系列答案

千里马口算天天练系列答案

小学毕业升学完全试卷系列答案

学情研测新标准系列答案

状元坊小学毕业总复习系列答案

语文阅读训练系列答案

点对点决胜中考系列答案

填充练习册系列答案

阅读导航系列答案

教材3D解读系列答案

通城学典默写能手系列答案

相关题目

11．已知$α∈（{0，\frac{π}{2}}）$，$β∈（{\frac{π}{2}，π}）$，$cosβ=-\frac{1}{3}$，$sin（{α+β}）=\frac{{4-\sqrt{2}}}{6}$．
（ I）求tan2β的值；
（ II）求α的值．

12．在四面体S-ABC中，若$SA=CB=\sqrt{5}$，$SB=AC=\sqrt{10}$，$SC=AB=\sqrt{13}$，则这个四面体的外接球的表面积为14π．

9．已知三棱锥S-ABC，其三视图中的正（主）视图和侧（左）视图如图所示，则该三棱锥的体积为（　　）

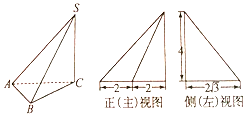
$\frac{{8\sqrt{3}}}{3}$

$\frac{{16\sqrt{3}}}{3}$

$\frac{{32\sqrt{3}}}{3}$

16．已知{a_n}是公差为2的等差数列，前5项和S₅=25，若a_2m=15，则m=（　　）

6．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{1}{2}$，它的一个焦点到短轴顶点的距离为2，动直线l：y=kx+m交椭圆E于A、B两点，设直线OA、OB的斜率都存在，且${k_{OA}}•{k_{OB}}=-\frac{3}{4}$．
（1）求椭圆E的方程；
（2）求证：2m²=4k²+3；
（3）求|AB|的最大值．

13．命题“?x∈Z，使x²+2x-1＜0”的否定为（　　）

	A．	?x∈Z，x²+2x-1≥0		B．	?x∈Z，使x²+2x-1＞0
	C．	?x∈Z，x²+2x+1＞0		D．	?x∈Z，使x²+2x-1≥0

10．已知等差数列{a_n}的前n项和为S_n，若$\frac{{a}_{5}}{{a}_{3}}$=$\frac{5}{9}$，则$\frac{{S}_{9}}{{S}_{5}}$=（　　）

11．为了在运行如图的程序之后输出的值为5，则输入x的所有可能的值是（　　）