题目内容
18.自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”、“不准备参加”和“待定”的人数如表:| 准备参加 | 不准备参加 | 待定 | |
| 男生 | 30 | 6 | 15 |
| 女生 | 15 | 9 | 25 |
(II)在“准备参加”自主招生的同学中用分层抽样方法抽取6人,从这6人中任意抽取2 人,求至少有一名女生的概率.
分析 (Ⅰ)根据分层抽样原理,分层抽样时的比值为$\frac{20}{100}=0.2$,即可求出在“准备参加”、“不准备参加”和“待定”的同学中应各抽取多少人;
(Ⅱ)求出所抽取的6人中男生应抽4人,女生抽2人,用列举法计算所有的基本事件数,求出对应的概率即可.
解答 解:(Ⅰ)分层抽样时的比值为$\frac{20}{100}=0.2$,-------------------(1分)
所以,在“准备参加”的同学中应抽取(30+15)×0.2=9(人),---------------------(2分)
在“不准备参加”的同学中应抽取(6+9)×0.2=3(人),---------------------(3分)
在“待定”的同学中应抽取(15+25)×0.2=8(人).---------------------(4分)
(Ⅱ)在“准备参加”自主招生的同学中用分层抽样方法抽取6人,
则男生应抽4人,女生抽2人,--------------------------------(5分)
男生4人分别记作1,2,3,4,女生2人分别记作5,6.
从6人中任取2人共有以下15种情况:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6).----------------------------------------(8分)
其中至少有一名女生的情况共有9种:(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),(5,6).-------------------------(10分)
所以,至少有一名女生的概率$P=\frac{9}{15}=0.6$.--------------------(12分)
点评 本题考查了分层抽样方法的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
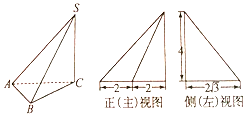
| A. | $\frac{{8\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $16\sqrt{3}$ |
| A. | ?x∈Z,x2+2x-1≥0 | B. | ?x∈Z,使x2+2x-1>0 | ||
| C. | ?x∈Z,x2+2x+1>0 | D. | ?x∈Z,使x2+2x-1≥0 |
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
| A. | $\frac{9}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |
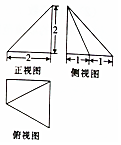
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |