题目内容
设数列{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b3=9,a5+b2=11
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ只限文班做)求数列{
}的前n项和Tn.
(Ⅱ只限理班做)求数列{
}的前n项和Tn.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ只限文班做)求数列{
| 1 |
| an•an+1 |
(Ⅱ只限理班做)求数列{
| an |
| bn |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用等差数列和等比数列的通项公式列出方程组,分别求出等差数列的公差和等比数列的公比,由此能求出数列{an},{bn}的通项公式.
(Ⅱ文科)由an=2n-1,利用裂项求和法能求出数列{
}的前n项和Tn.
(Ⅱ理科)由an=2n-1,bn=2n-1,得到
=
,利用错位相减法能求出数列{
}的前n项和Tn.
(Ⅱ文科)由an=2n-1,利用裂项求和法能求出数列{
| 1 |
| an•an+1 |
(Ⅱ理科)由an=2n-1,bn=2n-1,得到
| an |
| bn |
| 2n-1 |
| 2n-1 |
| an |
| bn |
解答:
解:(Ⅰ)设{an}的公差为d,{bn}的公比为q (q>0).
∵数列{an}是等差数列,{bn}是各项都为正数的等比数列,
且a1=b1=1,a3+b3=9,a5+b2=11,
∴
,
解得
,
∴an=2n-1,bn=2n-1.
(Ⅱ文科)∵an=2n-1,
∴Tn=
+
+…+
=
+
+
+…+
=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)
=
.
(Ⅱ理科)∵an=2n-1,bn=2n-1,
∴
=
,
∴Tn=
+
+
+…+
,①
则
Tn=
+
+…+
+
,②
由①-②得
Tn=
+
-
=1+
-
=3-
,
∴Tn=6-
.
∵数列{an}是等差数列,{bn}是各项都为正数的等比数列,
且a1=b1=1,a3+b3=9,a5+b2=11,
∴
|
解得
|
∴an=2n-1,bn=2n-1.
(Ⅱ文科)∵an=2n-1,
∴Tn=
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
=
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| (2n-1)×(2n+1) |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
(Ⅱ理科)∵an=2n-1,bn=2n-1,
∴
| an |
| bn |
| 2n-1 |
| 2n-1 |
∴Tn=
| 1 |
| 20 |
| 3 |
| 21 |
| 5 |
| 22 |
| 2n-1 |
| 2n-1 |
则
| 1 |
| 2 |
| 1 |
| 21 |
| 3 |
| 22 |
| 2n-3 |
| 2n-1 |
| 2n-1 |
| 2n |
由①-②得
| 1 |
| 2 |
| 1 |
| 20 |
| ||||||||
| 共n-1项 |
| 2n-1 |
| 2n |
=1+
(1-
| ||
1-
|
| 2n-1 |
| 2n |
| 3+2n |
| 2n |
∴Tn=6-
| 3+2n |
| 2n-1 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意裂项求和法和错位相减法的合理运用.

练习册系列答案
相关题目
对于每个非零自然数n,抛物线y=x2-
x+
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2014B2014的值是( )
| 2n+1 |
| n2+n |
| 1 |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b∈R且a≠b,若aea=beb(e为自然对数的底数),则下列正确的是( )
| A、lna-lnb=b-a |
| B、lna-lnb=a-b |
| C、ln(-a)-ln(-b)=b-a |
| D、ln(-a)-ln(-b)=a-b |
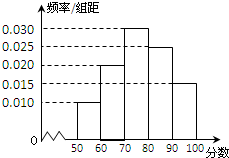 某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( ) 正四面体ABCD边长为2.E,F分别为AC,BD中点.
正四面体ABCD边长为2.E,F分别为AC,BD中点.