题目内容
设ξ为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,ξ=0,当四点不共面时,ξ的值为四点组成的四面体的体积.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:综合题,概率与统计
分析:(1)求出从正方体的八个顶点中任取四个点,共有
=70种情况,当四点共面时,共有12种情况,即可由概率公式求得概率.
(2)四点不共面时,四面体的体积有以下两种情况:①四点在相对面且异面的对角线上;②四点中有三个点在一个侧面上,另一个点在相对侧面上,求出相应的概率,从而求出随机变量的分布列与数学期望.
| C | 4 8 |
(2)四点不共面时,四面体的体积有以下两种情况:①四点在相对面且异面的对角线上;②四点中有三个点在一个侧面上,另一个点在相对侧面上,求出相应的概率,从而求出随机变量的分布列与数学期望.
解答:
解:(1)从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,共有
=70种情况,当四点共面时,共有12种情况,
∴P(ξ=0)=
=
.
(2)四点不共面时,四面体的体积有以下两种情况:
①四点在相对面且异面的对角线上,体积为1-4×
=
,这样的取法共有2种;
②四点中有三个点在一个侧面上,另一个点在相对侧面上,体积为
,这样的取法共有70-12-2=56种.
∴ξ的分布列为
数学期望E(ξ)=
×
+
×
=
.
| C | 4 8 |
∴P(ξ=0)=
| 12 |
| 70 |
| 6 |
| 35 |
(2)四点不共面时,四面体的体积有以下两种情况:
①四点在相对面且异面的对角线上,体积为1-4×
| 1 |
| 6 |
| 1 |
| 3 |
②四点中有三个点在一个侧面上,另一个点在相对侧面上,体积为
| 1 |
| 6 |
∴ξ的分布列为
| ξ | 0 |
|
| ||||||
| P |
|
|
|
| 1 |
| 3 |
| 1 |
| 35 |
| 1 |
| 6 |
| 28 |
| 35 |
| 1 |
| 7 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,求概率是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=
,则图中表示z的共轭复数的点是( )

| 2 |
| i-1 |

| A、A | B、B | C、C | D、D |
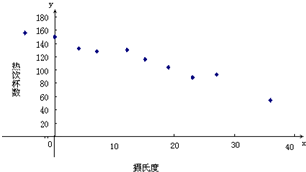 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程 |
| y |
| A、气温与热饮的销售杯数之间成正相关 | ||
| B、当天气温为2°C时,这天大约可以卖出143杯热饮 | ||
| C、当天气温为10°C时,这天恰卖出124杯热饮 | ||
D、由于x=0时,
|