题目内容
已知偶函数f（x）满足f（x-1）=f（x+1），且当x∈[0，1]时，f（x）=x2，求方程f（x）=（
）x在[0，
]上的实根个数．
| 1 |
| 10 |
| 10 |
| 3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：首先，根据f（x+1）=f（x-1），得到函数f（x）的周期为2，然后，在同一坐标系中画出在[0，
]上的函数y=f（x）和y=（
）x的简图，根据图象，容易得到结果．
| 10 |
| 3 |
| 1 |
| 10 |
解答：
解：∵f（x+1）=f（x-1），
∴f（x+2）=f（x），
∴函数f（x）的周期为2，
在[0，
]上，函数y=f（x）和y=（
）x的简图：
根据图象，知关于x的方程f（x）=（
）x在[0，
]上的实根个数是3．
∴f（x+2）=f（x），
∴函数f（x）的周期为2，
在[0，
| 10 |
| 3 |
| 1 |
| 10 |
根据图象，知关于x的方程f（x）=（
| 1 |
| 10 |
| 10 |
| 3 |
点评：本题重点考查了偶函数的性质、周期函数的概念、函数的基本性质等知识，属于中档题．
练习册系列答案
相关题目
已知集合A={x∈R|y=
}，B={y∈R|y=
}，则A∩B=（ ）
| 1-x |
| x-1 |
| A、∅ | B、{1} |
| C、[0，1] | D、{（1，0）} |
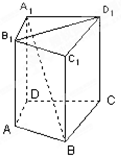如图，在直四棱柱A1B1C1D1-ABCD中，当底面四边形ABCD满足条件