题目内容
19.已知函数f(x)=x3-6x2+3x+t,(t∈R).(1)求函数f(x)的单调递减区间;
(2)若函数g(x)=exf(x)只有一个极值点,求t的取值范围.
分析 (1)令f′(x)=3x2-12x+3<0,可求函数f(x)的单调递减区间;
(2)求导函数,f′(x)=(3x2-12x+3)ex+(x3-6x2+3x+t)ex=(x3-3x2-9x+t+3)ex,函数g(x)=exf(x)有一个极值点,所以x3-3x2-9x+t+3=0有一个穿过x轴的根,即在其两边g'(x)异号,故可求t的取值范围.
解答 解:(1)令f'(x)=3x2-12x+3<0,
∴2-$\sqrt{3}$<x<2+$\sqrt{3}$,
∴函数f(x)的单调递减区间是(2-$\sqrt{3}$,2+$\sqrt{3}$);(5分)
(2)g'(x)=(3x2-12x+3)ex+(x3-6x2+3x+t)ex=(x3-3x2-9x+t+3)ex
∵g(x)有一个极值点,
∴x3-3x2-9x+t+3=0有一个穿过x轴的根,即在其两边g'(x)异号-----------------------------------(8分)
令h(x)=x3-3x2-9x+t+3,则h'(x)=3x2-6x-9=3(x+1)(x-3)
由h'(x)=3x2-6x-9=3(x+1)(x-3)>0得x<-1或x>3…(10分)
h(x)在区间(-∞,-1)和(3,+∞)上递增,在区间(-1,3)上递减.
∴h(-1)h(3)≥0∴t≤-8或t≥24.…(12分)
点评 本题考查函数的极值和单调性的应用,考查利用导数求函数的单调性,考查函数的极值,解题的关键是将函数g(x)=exf(x)有一个极值点,转化为x3-3x2-9x+t+3=0有一个穿过x轴的根,即在其两边g'(x)异号.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.定义在R上的函数y=f(x)为减函数,且函数y=f(x-1)的图象关于点(1,0)对称,若f(x2-2x)+f(2b-b2)≤0,且0≤x≤2,则x-b的取值范围是( )
| A. | [-2,0] | B. | [-2,2] | C. | [0,2] | D. | [0,4] |
11.若实数x,y满足$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$则z=x-ay只在点(4,3)处取得最大值,则a的取值范围为( )
| A. | (-∞,0)∪(1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,1) |
8.已知i是虚数单位,若$\frac{1+2i}{z}$=2-i,则z的模为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | i | D. | 1 |
9.若圆(x-1)2+(y-4)2=4的圆心到直线ax+y-1=0的距离为1,则a=( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
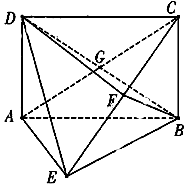 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G. 已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.
已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.