题目内容
15.已知4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=sin2θ,则tan(2θ-$\frac{π}{6}$)等于( )| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
分析 根据诱导公式和二倍角公式,以及两角差的正切公式计算即可.
解答 解:由已知得4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=-4sin(θ-$\frac{π}{6}$)cos(θ-$\frac{π}{6}$)
=-2sin(2θ-$\frac{π}{3}$)=-sin2θ+$\sqrt{3}$cos2θ=sin2θ,
即tan2θ=$\frac{\sqrt{3}}{2}$,
∴tan(2θ-$\frac{π}{6}$)=$\frac{\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{3}}{1+\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{9}$.
故选:B
点评 本题考查了诱导公式和二倍角公式,以及两角差的正切公式,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.复数z满足(z-i)(2-i)=5,则z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.设x,y满足不等式组$\left\{\begin{array}{l}{x+y-6≤0}\\{x-y-2≤0}\\{x≥0}\end{array}\right.$,则z=-2x+y的最小值为-6.
3.已知sinα+cosα=$\frac{1-\sqrt{3}}{2}$,且0<α<π,则tanα的值为( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
20.已知球的直径SC=2,A,B是该球球面上的两点,AB=1,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( )
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
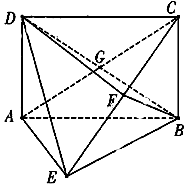 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G. 已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.
已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.