题目内容
14.从2名语文老师,2名数学老师,4名英语老师中选派5人组成一个支教小组,则语文老师、数学老师、英语老师都至少有一人的选派方法种数为44.(用数字作答)分析 根据题意,按4种情况讨论,分别求出每种情况下的选派方法数目,最后由分步计数原理计算可得答案
解答 解:根据题意,按4种情况讨论:
①、2名语文老师,2名数学老师,1名英语老师,有C41=4种,
②、1名语文老师,2名数学老师,2名英语老师,有C21C42=12种,
③、2名语文老师,1名数学老师,2名英语老师,有C21C42=12种,
④,1名语文老师,1名数学老师,3名英语老师,有C21C21C43=16种,
则一共有4+12+12+16=44种选派方法,
故答案为:44
点评 本题主要考查了排列、组合及简单计数问题,解答关键是利用直接法:先分类后分步.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
2.已知a,b均为实数,则“ab2>1”是“a>$\frac{1}{{b}^{2}}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.抛物线y2-4x=0上一点P到焦点的距离为3,那么P的横坐标是( )
| A. | 3 | B. | 2 | C. | $\frac{5}{2}$ | D. | -2 |
3.如果一个函数f(x)在定义域D中满足:①存在x1,x2∈D,且x1≠x2,使得f(x1)=f(x2);②任意x1,x2∈D,f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$,则f(x)可以是( )
| A. | f(x)=log2x | B. | f(x)=-x2+2x | C. | f(x)=2|x| | D. | f(x)=sinx |
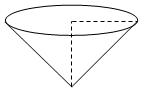 用铁皮制作一个容积为$\frac{1000π}{3}$cm3的无盖圆锥形容器,如图,若圆锥的母线与底面所称的角为45°,求制作该容器需要多少面积的铁皮(铁皮街接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个容积为$\frac{1000π}{3}$cm3的无盖圆锥形容器,如图,若圆锥的母线与底面所称的角为45°,求制作该容器需要多少面积的铁皮(铁皮街接部分忽略不计,结果精确到0.1cm2)