题目内容
19.已知角θ的始边与x轴的非负半轴重合,终边在y=$\frac{1}{2}$x上,则tan2θ=$\frac{4}{3}$.分析 利用直线斜率的定义、二倍角的正切公式,进行计算即可.
解答 解:∵角θ的始边与x轴的非负半轴重合,终边在直线y=$\frac{1}{2}$x上,
∴tanθ=$\frac{1}{2}$;
∴tan2θ=$\frac{2tanθ}{1{-tan}^{2}θ}$=$\frac{2×\frac{1}{2}}{1{-(\frac{1}{2})}^{2}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了直线斜率的定义与二倍角的正切公式的应用问题,是基础题目.

练习册系列答案
相关题目
4.抛物线y2=-4x的焦点坐标是( )
| A. | (-2,0) | B. | (-1,0) | C. | (0,-1) | D. | (0,-2) |
11.已知函数y=f(x-l)+x2是定义在R上的奇函数,若f(-2)=1,则f(0)=( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
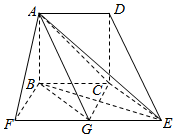 如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=$\frac{1}{2}$EF.
如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=$\frac{1}{2}$EF.