题目内容
6．抛物线y2-4x=0上一点P到焦点的距离为3，那么P的横坐标是（ ）| A． | 3 | B． | 2 | C． | $\frac{5}{2}$ | D． | -2 |
分析 由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，已知|PF|=3，则P到准线的距离也为6，即点M的横坐标x+$\frac{p}{2}$=3，将p的值代入，进而求出x．
解答 解：∵抛物线y2=4x=2px，
∴p=2，
由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，
∴|PF|=3；x+$\frac{p}{2}$=3，
∴x=2，
故选：B．
点评 活用抛物线的定义是解决抛物线问题最基本的方法．抛物线上的点到焦点的距离，叫焦半径．到焦点的距离常转化为到准线的距离求解．
练习册系列答案
阅读快车系列答案
相关题目
16．已知集合A={0，1，2}，B={x|y=lnx}，则A∩B=（ ）
| A． | {0，2} | B． | {0，1} | C． | {1，2} | D． | {0，1，2} |
17．
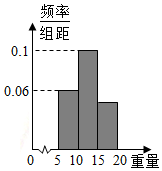从一批待测物品中随机抽测100件的重量（单位：kg），将所得数据绘制成如图所示的频率分布直方图，估计这批物品的平均重量（单位：kg）为（ ）
从一批待测物品中随机抽测100件的重量（单位：kg），将所得数据绘制成如图所示的频率分布直方图，估计这批物品的平均重量（单位：kg）为（ ）| A． | 11 | B． | 11.5 | C． | 12 | D． | 12.5 |
11．已知函数y=f（x-l）+x2是定义在R上的奇函数，若f（-2）=1，则f（0）=（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
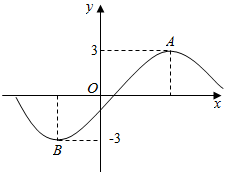已知函数f（x）=3sin（ωx+φ）（ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，A、B两点之间的距离为10，且f（2）=0，若将函数f（x）的图象向右平移t（t＞0）个单位长度后所得函数图象关于y轴对称，则t的最小值为6．