题目内容
3.已知定义在R上的函数f(x),对任意实数x满足f(x+2)=-f(x-2),且当x∈[0,8)时,f(x)=2x-10,则f(2015)=4.分析 由题意可得函数的周期为8,结合当x∈[0,8)时,f(x)=2x-10,可得答案.
解答 解:∵f(x+2)=-f(x-2),
∴f(x+4)=-f[(x+2)-2]=-f(x)
∴f(x+8)=-f(x+4)=f(x),
∴函数f(x)是周期为8的周期函数,
∴f(2015)=f(256×8+7)=f(7),
又∵当x∈[0,8)时,f(x)=2x-10,
∴f(7)=14-10=4,
∴f(2015)=4.
故答案为:4.
点评 本题考查抽象函数的应用,考查函数的周期性,属基础题.

练习册系列答案
相关题目
13.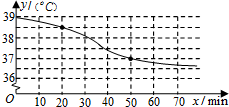 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )| A. | 0.05(℃/min) | B. | -0.05(℃/min) | C. | 0.025(℃/min) | D. | -0.025(℃/min) |
14.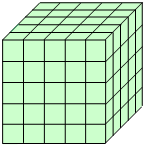 如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )
如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )
 如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )
如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )| A. | $\frac{12}{125}$ | B. | $\frac{27}{125}$ | C. | $\frac{98}{125}$ | D. | $\frac{168}{125}$ |
11.函数f(x)=5cos(4x+$\frac{π}{4}$)的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
18.下面四个图象中,符合函数y=-xsinx的图象是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知中心在原点,焦点F1、F2在x轴上的双曲线经过点P(4,2),△PF1F2的内切圆与x轴相切于点Q(2$\sqrt{2}$,0),则双曲线的实轴长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
 如图,在体积为16的正四棱柱ABCD-A1B1C1D1中,点M是DD1的中点,DD1=2AD.
如图,在体积为16的正四棱柱ABCD-A1B1C1D1中,点M是DD1的中点,DD1=2AD.