题目内容
8.已知中心在原点,焦点F1、F2在x轴上的双曲线经过点P(4,2),△PF1F2的内切圆与x轴相切于点Q(2$\sqrt{2}$,0),则双曲线的实轴长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 根据三角形内切圆的性质结合双曲线的定义,求出2a,即可得到结论.
解答 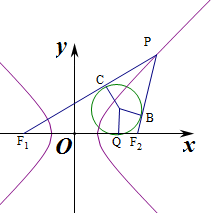 解:中心在原点,焦点F1、F2在x轴上的双曲线为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
解:中心在原点,焦点F1、F2在x轴上的双曲线为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
作出对应的图象如图:设三个切点分别为A,B,C,
∵△PF1F2的内切圆与x轴相切于点Q(2$\sqrt{2}$,0),
∴|F1Q|=|F1C|=c+2$\sqrt{2}$,∴|F2Q|=|F2B|=c-2$\sqrt{2}$,
∴由双曲线的定义得||F1P|-|F2P|=|F1C|-|F2B|=c+2$\sqrt{2}$-(c-2$\sqrt{2}$)=4$\sqrt{2}$=2a,
故选:D.
点评 本题主要考查双曲线的实轴长的计算,根据三角形内切圆的性质求出2a是解决本题的关键.注意利用数形结合进行求解.

练习册系列答案
相关题目
20.直线x+(m+1)y+3=0与直线mx+2y-1=0平行,则m的值为( )
| A. | 1 | B. | -2 | C. | 2或-1 | D. | -2或1 |
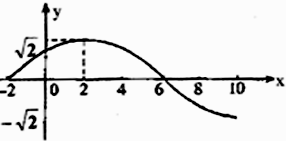 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示: