题目内容
13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1的离心率为$\sqrt{3}$，则它的渐近线方程是y=±$\sqrt{2}$x．分析 由离心率公式解出a，再由双曲线方程写出渐近线方程即可．
解答 解：双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1的离心率为$\sqrt{3}$，
∴e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+2}}{a}$=$\sqrt{3}$，
∴解得a=1，
∴双曲线的渐近线方程为y=±$\sqrt{2}$x，
故答案为：y=±$\sqrt{2}$x．
点评 本题考查双曲线的方程和性质，考查双曲线的离心率与渐近线方程，考查运算能力，属于基础题．
练习册系列答案
相关题目
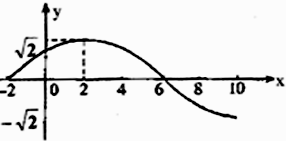已知函数$f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示：