题目内容
14．
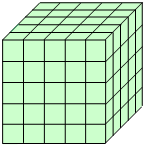如图，将一个各面都涂了油漆的正方体，切割成125个同样大小的小正方体．经过搅拌后，从中随机取出一个小正方体，则取到含油漆的概率为（ ）| A． | $\frac{12}{125}$ | B． | $\frac{27}{125}$ | C． | $\frac{98}{125}$ | D． | $\frac{168}{125}$ |
分析 正确找出六个面都没有涂漆的小正方体，继而得到涂了油漆小正方体，再利用古典概型的概率计算公式即可得出．
解答 解：把一个正方体各个面都涂上漆，之后分为125个大小相等的小正方体，
可知只有3×3×3=27个小正方体各个面都没有涂漆，
故它涂了油漆的得小正方体有125-27=98，
故从中随机取出一个小正方体，则它涂了油漆的概率P=$\frac{98}{125}$，
故选：C．
点评 本题主要考查了古典概型的概率计算公式，关键是正确找出六个面都没有涂漆的小正方体，属于基础题．
练习册系列答案
相关题目
4．某酒店连续5个月的销售额和利润额资料如下表：
（Ⅰ）画出销售额和利润额的散点图；
（Ⅱ）如果y对x有线性相关关系，求回归直线方程$\widehat{y}$=bx+a；
（Ⅲ）如果要求该酒店的利润每月不能少于3.4万元，请你估计一下，这个酒店每月的销售额不得少于多少万元？（参考公式b=$\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$）．
| 销售额（x）/万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额（y）/万元 | 2 | 3 | 3 | 4 | 5 |
（Ⅱ）如果y对x有线性相关关系，求回归直线方程$\widehat{y}$=bx+a；
（Ⅲ）如果要求该酒店的利润每月不能少于3.4万元，请你估计一下，这个酒店每月的销售额不得少于多少万元？（参考公式b=$\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$）．