题目内容
给定集合A,B,定义一种新运算:A⊕B={x|x∈A或x∈B,但x∉A∩B},又已知A={0,1,2},B={1,2,3},则A⊕B= .
考点:元素与集合关系的判断
专题:规律型
分析:根据集合的新定义,计算出集合交集和并集,件即可确定集合的元素即可.
解答:
解:∵A={0,1,2},B={1,2,3},
∴A∪B={0,1,2,3},A∩B={1,2},
∴A⊕B={x|x∈A或x∈B,但x∉A∩B}={0,3},
故答案:{0,3}.
∴A∪B={0,1,2,3},A∩B={1,2},
∴A⊕B={x|x∈A或x∈B,但x∉A∩B}={0,3},
故答案:{0,3}.
点评:本题主要考查集合元素的确定,利用定义直接求解即可,比较基础.

练习册系列答案
相关题目
已知条件p:x2-3x-4≤0,条件q:x2-6x+9-m2≤0(m>0).若p是q的充分不必要条件,则正数m的取值范围为( )
| A、(0,1] |
| B、(0,4] |
| C、[1,+∞) |
| D、[4,+∞) |
 已知函数f(x)=
已知函数f(x)=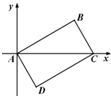 如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,