题目内容
如果实数x,y满足等式(x-2)2+y2=3,那么
的最大值是( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:圆的标准方程
专题:计算题,直线与圆
分析:
表示圆上动点与原点O连线的斜率,画出满足等式(x-2)2+y2=3的图形,由数形结合,我们易求出
的最大值.
| y |
| x |
| y |
| x |
解答:
 解:满足等式(x-2)2+y2=3的图形如图所示:
解:满足等式(x-2)2+y2=3的图形如图所示:
表示圆上动点与原点O连线的斜率,
由图可得动点与B重合时,此时OB与圆相切
取最大值,
连接BC,在Rt△OBC中,BC=
,OC=2
易得∠BOC=60°
此时
=
故选:A.
 解:满足等式(x-2)2+y2=3的图形如图所示:
解:满足等式(x-2)2+y2=3的图形如图所示:| y |
| x |
由图可得动点与B重合时,此时OB与圆相切
| y |
| x |
连接BC,在Rt△OBC中,BC=
| 3 |
易得∠BOC=60°
此时
| y |
| x |
| 3 |
故选:A.
点评:本题考查的知识点是圆的标准方程,分析出
表示圆上动点与原点O连线的斜率,是解答本题的关键.
| y |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知M={y|y=x2,x∈R},N={y|x2+y2=1,x∈R,y∈R},则M∩N=( )
| A、[-2,2] |
| B、[0,2] |
| C、[0,1] |
| D、[-1,1] |
若方程
-
=1表示双曲线,则k的取值范围是( )
| x2 |
| k |
| y2 |
| k-2 |
| A、k>2 | B、k<0 |
| C、k>2,或k<0 | D、0<k<2 |
与双曲线x2-
=1有共同渐近线,且过点(2,
)的双曲线方程是( )
| y2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}的通项公式为an=(-1)n+1•
,则a7=( )
| n+1 |
| n |
| A、8 | ||
B、-
| ||
C、
| ||
| D、7 |
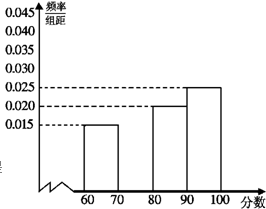 某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:
某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表: