题目内容
已知函数f(x)=2cosx(sinx+cosx)+m,(m∈R),在区间[0,
]内最大值为
,
(1)求实数m的值;
(2)在△ABC中,三内角A、B、C所对边分别为a,b,c,且f(
B)=1,a+c=2,求b的取值范围.
| π |
| 4 |
| 2 |
(1)求实数m的值;
(2)在△ABC中,三内角A、B、C所对边分别为a,b,c,且f(
| 3 |
| 4 |
考点:正弦定理的应用,两角和与差的正弦函数
专题:三角函数的求值
分析:(1)利用函数的解析式通过二倍角公式以及两角和的正弦函数化简函数的解析式,通过正弦函数的最值,求实数m的值;
(2)利用f(
B)=1,求出B的值,通过a+c=2以及正弦定理,直接求b的表达式,通过A的范围集合正弦函数的值的范围,求解b取值范围.
(2)利用f(
| 3 |
| 4 |
解答:
解:(1)f(x)=2cosx(sinx+cosx)+m
=2cosxsinx+2cos2x+m
=sin2x+cos2x+m+1
=
sin(2x+
)+m+1,
当x∈[0,
]时,
sin(2x+
)最大值为
,
在区间[0,
]内函数的最大值为
,
∴
+m+1=
∴m=-1
(2)f(
B)=1⇒
sin(
B+
)=1⇒
B+
=
,(∵0<B<π)
解得B=
由正弦定理得:b=
•sinB=
•
sinA+sin(
-A)=sinA+
cosA+
sinA=
(
sinA+
cosA)=
sin(A+
)
∴
<sinA+sin(
-A)≤
,(当A=
时取最大值
)
∴1≤b<2,(当△ABC为正三角形时,b=1)
=2cosxsinx+2cos2x+m
=sin2x+cos2x+m+1
=
| 2 |
| π |
| 4 |
当x∈[0,
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
在区间[0,
| π |
| 4 |
| 2 |
∴
| 2 |
| 2 |
∴m=-1
(2)f(
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
解得B=
| π |
| 3 |
| a+c |
| sinA+sinC |
| ||
| 2 |
| 2 | ||
sinA+sin(
|
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
∴
| ||
| 2 |
| 2π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
∴1≤b<2,(当△ABC为正三角形时,b=1)
点评:本题考查两角和与差的三角函数,二倍角公式的应用,正弦定理的应用,考查转化思想以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=
的最小值为-1,则实数a取值范围( )
|
A、{a|a≥-
| ||
B、{a|a>-
| ||
C、{a|a<-
| ||
| D、{a|a≥-1} |
已知O为坐标原点,
=(x,y),
=(a,0),
=(0,a),
=(3,4),记|
|、|
|、|
|中的最大值为M,当a取遍一切实数时,M的取值范围是( )
| OP |
| OA |
| OB |
| OC |
| PA |
| PB |
| PC |
A、[
| ||
B、[7+2
| ||
C、[7-2
| ||
D、[7,7+2
|
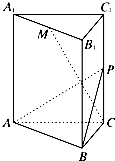 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2