Question

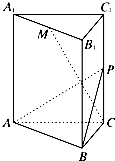如图，三棱柱ABC-A₁B₁C₁的底面是边长为4正三角形，AA₁⊥平面ABC，AA₁=2

6

，M为A₁B₁的中点．
（Ⅰ）求证：MC⊥AB；
（Ⅱ）若点P为CC₁的中点，求二面角B-AP-C的余弦值．

Answer 1

考点：二面角的平面角及求法,空间中直线与直线之间的位置关系

专题：计算题,作图题,空间位置关系与距离,空间向量及应用

分析：（Ⅰ）取AB中点O，连接OM，OC，可证MO⊥AB，AB⊥CO，从而可证AB⊥平面OMC，从而可证MC⊥AB；
（Ⅱ）以O为原点，以

OB

，

OC

，

OM

的方向分别为x轴，y轴，z轴的正方向，建立空间直角坐标系．如图．依题意O（0，0，0），A（-2，0，0），B（2，0，0），C（0，2

3

，0），M（0，0，2

6

），P（0，2

3

，

6

）；从而求得

DB

=（3，-

3

，0）为平面PAC的一个法向量，

MC

=（0，2

3

，-2

6

）为平面PAB的一个法向量；从而求二面角B-AP-C的余弦值．

解答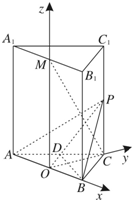： 解：（I）取AB中点O，连接OM，OC．
∵M为A₁B₁中点，
∴MO∥A₁A，
又∵A₁A⊥平面ABC，
∴MO⊥平面ABC，
∴MO⊥AB；
∵△ABC为正三角形，
∴AB⊥CO，
又∵MO∩CO=O，
∴AB⊥平面OMC．
又∵MC?平面OMC，
∴AB⊥MC．
（II）以O为原点，以

OB

，

OC

，

OM

的方向分别为x轴，y轴，z轴的正方向，建立空间直角坐标系．
如图．依题意O（0，0，0），A（-2，0，0），B（2，0，0），C（0，2

3

，0），M（0，0，2

6

），P（0，2

3

，

6

）；
∴当P为线段CC₁的中点时，MC⊥平面ABP．
取线段AC的中点D，则D（-1，

3

，0），
易知DB⊥平面A₁ACC₁，
故

DB

=（3，-

3

，0）为平面PAC的一个法向量．
又由（II）知

MC

=（0，2

3

，-2

6

）为平面PAB的一个法向量．
设二面角B-AP-C的平面角为α，
则|cosα|=

| MC • DB |

| MC |•| DB |

=|

3×0- 3 ×2 3 -0×2 6

2 3 ×6

=

3

6

．
故二面角B-AP-C的余弦值为

3

6

．

点评：本题考查了异面直线垂直的证明，用到了线面垂直的判定与性质定理，同时考查了空间向量的应用，属于难题．