题目内容
9.自点(-3,3)发出的光线射到x轴上,被x轴反射,其反射光线L所在直线与圆x2+y2-4x-4y+7=0相切,则反射光线L所在直线方程为4x-3y+3=0或3x-4y-3=0.分析 化简圆的方程为标准方程,求出关于x轴对称的圆的方程,设l的斜率为k,利用相切求出k的值即可得反射光线所在的直线方程.
解答 解:如图示: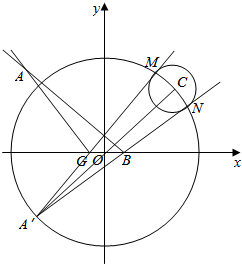
根据对称关系,首先求出点A的对称点A′的坐标为(-3,-3),
其次设过A′的圆C的切线方程为y=k(x+3)-3
根据d=$\frac{|5k-5|}{\sqrt{{k}^{2}+1}}$=1,即求出圆C的切线的斜率为k=$\frac{4}{3}$或k=$\frac{3}{4}$,
进一步求出反射光线所在的直线的方程为:
4x-3y+3=0或3x-4y-3=0,
故答案为:4x-3y+3=0或3x-4y-3=0.
点评 本题考查点、直线和圆的对称问题,直线与圆的关系,是基础题.

练习册系列答案
相关题目
1.设函数y=f(x)在x=x0处可导,且$\underset{lim}{△x→0}$$\frac{f({x}_{0}-3△x)-f({x}_{0})}{2△x}$=1,则f′(x0)等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | 1 | D. | -1 |
18.定义:若函数y=f(x)的图象上存在两个不同的点A,B,使得函数f(x)的图象上在这两点处的切线关于垂直于x轴的某条直线对称,则称函数y=f(x)为D函数.下列选项是D函数的为( )
| A. | y=x3 | B. | y=cosx | C. | y=lnx | D. | y=ex |