题目内容
18．定义：若函数y=f（x）的图象上存在两个不同的点A，B，使得函数f（x）的图象上在这两点处的切线关于垂直于x轴的某条直线对称，则称函数y=f（x）为D函数．下列选项是D函数的为（ ）| A． | y=x3 | B． | y=cosx | C． | y=lnx | D． | y=ex |
分析 由题意，f（x）的导函数上存在两点，使这两点的导函数值互为相反数，然后对四个函数逐一求导判断．
解答 解：函数y=f（x）的图象上存在两个不同的点A，B，使得函数f（x）的图象上在这两点处的切线关于垂直于x轴的某条直线对称，说明f（x）的导函数上存在两点，使这两点的导函数值互为相反数．
当y=x3时，y′=3x2≥0，不满足题意；
当y=cosx时，y′=-sinx，满足题意；
当y=lnx时，y′=$\frac{1}{x}＞0$，不满足题意；
当y=ex时，y′=ex＞0，不满足题意．
故选：B．
点评 本题考查利用导数研究过曲线上某点处的切线方程，关键是明确函数在某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
如图，∠ACB=90°，DA⊥平面ABC，AE⊥DB交DB于E，AF⊥DC交DC于F，且AD=AB=2，则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$．
6．双曲线 $\frac{x^2}{{1+{k^2}}}-\frac{y^2}{{8-{k^2}}}=1$（k为常数）的焦点坐标是（ ）
| A． | （0，±3） | B． | （±3，0） | C． | （±1，0） | D． | （0，±1） |
13．已知△ABC，A，B，C所对的边分别为a，b，c，且acsinA＜$\overrightarrow{BA}•\overrightarrow{BC}$，则（ ）
| A． | △ABC是钝角三角形 | B． | △ABC是锐角三角形 | ||
| C． | △ABC是直角三角形 | D． | 无法判断 |
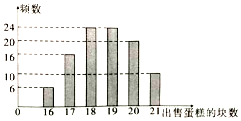某蛋糕店出售一种蛋糕，这种蛋糕的保质期很短，必须当天卖掉，否则容易变质，该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块，然后以每块26元的价格出售，如果当天卖不完，剩下的蛋糕只能以每块6元低价出售．蛋糕店记录了100天该种蛋糕的日需求量n（单位：块，n∈N*）整理得如图：
17．已知两条不同直线a，b及平面α，则下列命题中真命题是（ ）
| A． | 若a∥α，b∥α，则a∥b | B． | 若a∥b，b∥α，则a∥α | C． | 若a⊥α，b⊥α，则a∥b | D． | 若a⊥α，b⊥a，则b⊥α |