题目内容
8.已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试分别确定m、n的值,使:(1)l1与l2相交于点P(3,1);
(2)l1∥l2;
(3)l1⊥l2且l1在y轴上的截距为-1.
分析 (1)由l1与l2相交于点P(3,1),可得$\left\{\begin{array}{l}{3m+8+n=0}\\{6+m-1=0}\end{array}\right.$,解出m,n,即可得出.
(2)由m2-2×8=0,解得m=±4,经过检验即可得出.
(3)m=0时,两条直线分别化为:8y+n=0,2x-1=0,此时两条直线相互垂直;m≠0时,由于两条直线相互垂直可得:$-\frac{m}{8}×(-\frac{2}{m})$=-1,解出即可判断出结论.
解答 解:(1)∵l1与l2相交于点P(3,1),∴$\left\{\begin{array}{l}{3m+8+n=0}\\{6+m-1=0}\end{array}\right.$,解得m=-5,n=7.
(2)由m2-2×8=0,解得m=±4,经过检验可得:m=4,n≠-2时两条直线平行;m=-4,n≠2时两条直线平行.
(3)m=0时,两条直线分别化为:8y+n=0,2x-1=0,此时两条直线相互垂直;
m≠0时,由于两条直线相互垂直可得:$-\frac{m}{8}×(-\frac{2}{m})$=-1,无解.
综上可得:只有m=0时,两条直线相互垂直.
点评 本题考查了相互平行与垂直的直线斜率之间的关系、分类讨论方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
13.设Sn为等差数列{an}的前n项和,a1=-2,S3=0,则{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中不正确的序号有( )
①若α⊥β,α∩β=m,且n⊥m,则n⊥α或n⊥β
②若m不垂直于α,则m不可能垂直于α内的无数条直线
③若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β
④若α⊥β,m∥n,n⊥β,则m∥α
①若α⊥β,α∩β=m,且n⊥m,则n⊥α或n⊥β
②若m不垂直于α,则m不可能垂直于α内的无数条直线
③若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β
④若α⊥β,m∥n,n⊥β,则m∥α
| A. | ①②③④ | B. | ③ | C. | ①④ | D. | ①②④ |
17.已知两条不同直线a,b及平面α,则下列命题中真命题是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥b,b∥α,则a∥α | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a⊥α,b⊥a,则b⊥α |
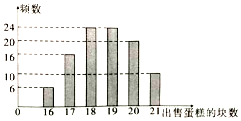 某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:
某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: