题目内容
1．设函数y=f（x）在x=x0处可导，且$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-3△x）-f（{x}_{0}）}{2△x}$=1，则f′（x0）等于（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{3}{2}$ | C． | 1 | D． | -1 |
分析 变形利用导数的运算定义即可得出．
解答 解：∵$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-3△x）-f（{x}_{0}）}{2△x}$=（-$\frac{3}{2}$）$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-3△x）-f（{x}_{0}）}{-3△x}$=（-$\frac{3}{2}$）f′（x0）=1，
∴f′（x0）=-$\frac{2}{3}$，
故选A．
点评 本题考查了导数的运算定义，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
16．下列有关命题的说法正确的是（ ）
| A． | “x2=1”是“x=1”的充分不必要条件 | |
| B． | “x=2时，x2-3x+2=0”的否命题为真命题 | |
| C． | 命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” | |
| D． | 命题“若x=y，则sinx=siny”的逆否命题为真命题 |
6．双曲线 $\frac{x^2}{{1+{k^2}}}-\frac{y^2}{{8-{k^2}}}=1$（k为常数）的焦点坐标是（ ）
| A． | （0，±3） | B． | （±3，0） | C． | （±1，0） | D． | （0，±1） |
13．已知△ABC，A，B，C所对的边分别为a，b，c，且acsinA＜$\overrightarrow{BA}•\overrightarrow{BC}$，则（ ）
| A． | △ABC是钝角三角形 | B． | △ABC是锐角三角形 | ||
| C． | △ABC是直角三角形 | D． | 无法判断 |
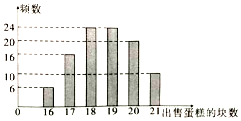某蛋糕店出售一种蛋糕，这种蛋糕的保质期很短，必须当天卖掉，否则容易变质，该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块，然后以每块26元的价格出售，如果当天卖不完，剩下的蛋糕只能以每块6元低价出售．蛋糕店记录了100天该种蛋糕的日需求量n（单位：块，n∈N*）整理得如图：