题目内容
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右两个焦点分别为F1,F2,M为圆x2+y2=$\frac{{a}^{2}}{4}$上的点,过左焦点F1与点M的直线交双曲线右支于点P,若M为线段PF1的中点,当△PF1F2为锐角三角形时,双曲线的离心率范围为$(\sqrt{2},\frac{\sqrt{10}}{2})$.分析 如图所示,M为线段PF1的中点,O为F1F2的中点,可得|PF2|=2|MO|=a,|PF1=|PF2|+2a=3a.当△PF1F2为锐角三角形时,∴只有可能∠PF2F1或∠F1PF2为最大角,因此必然为锐角.利用余弦定理即可得出.
解答 解:如图所示,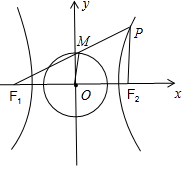
∵M为线段PF1的中点,O为F1F2的中点,
∴|PF2|=2|MO|=a,|PF1=|PF2|+2a=3a.
|F1F2|=2c.
∵当△PF1F2为锐角三角形时,∴只有可能∠PF2F1或∠F1PF2为最大角,因此必然为锐角.
∴(2c)2+a2>(3a)2,且(3a)2+a2>(2c)2,
可得c2>2a2,且${c}^{2}<\frac{5}{2}{a}^{2}$
解得$\sqrt{2}<e<\frac{\sqrt{10}}{2}$
故答案为:$(\sqrt{2},\frac{\sqrt{10}}{2})$.
点评 本题考查了双曲线的标准方程及其性质、三角形中位线定理、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=sin(2x+ϕ)(其中ϕ是实数),若$f(x)≤|{f({\frac{π}{6}})}|$对x∈R恒成立,且$f({\frac{π}{2}})>f(0)$,则f(x)的单调递增区间是( )
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | $[{kπ,kπ+\frac{π}{2}}]({k∈Z})$ | C. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]({k∈Z})$ | D. | $[{kπ-\frac{π}{2},kπ}]({k∈Z})$ |
7.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数f(x)=3sin2x的值不小于0的概率为( )
| A. | $\frac{6}{11}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{12}$ |
14.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F作斜率为1的直线交椭圆于A,B两点.若向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与向量$\overrightarrow{a}$=(3,-1)共线,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
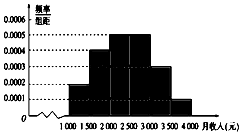 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500). 如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$.
如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$.