题目内容
 如图,四棱锥E-ABCD,底面ABCD是矩形,平面EDC⊥底面ABCD,ED=EC=BC=4,CF⊥平面BDE,且点F在EB上.
如图,四棱锥E-ABCD,底面ABCD是矩形,平面EDC⊥底面ABCD,ED=EC=BC=4,CF⊥平面BDE,且点F在EB上.(Ⅰ)求证:DE⊥平面BCE;
(Ⅱ)求三棱锥A-BDE的体积;
(Ⅲ)设点M在线段DC上,且满足DM=2CM,试在线段EB上确定一点N,使得MN∥平面ADE.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明DE⊥平面BCE,只需证明DE⊥BC,ED⊥CF;
(Ⅱ)过点E作EH⊥DC,利用VA-BDE=VE-ABD,即可求三棱锥A-BDE的体积;
(Ⅲ)过M作MG∥DE交CE于G,过G作GN∥BC交EB于N,连接MN,证明MN∥平面ADE,即可得出结论.
(Ⅱ)过点E作EH⊥DC,利用VA-BDE=VE-ABD,即可求三棱锥A-BDE的体积;
(Ⅲ)过M作MG∥DE交CE于G,过G作GN∥BC交EB于N,连接MN,证明MN∥平面ADE,即可得出结论.
解答:
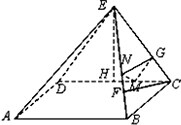 (Ⅰ)证明:∵ABCD是矩形,
(Ⅰ)证明:∵ABCD是矩形,
∴BC⊥DC,
∵平面EDC⊥底面ABCD,平面EDC∩底面ABCD=DC,BC⊥DC,
∴BC⊥平面EDC,
∴DE⊥BC,
∵CF⊥平面BDE,
∴ED⊥CF,
∵BC∩CF=C,DE⊥BC,ED⊥CF,
∴DE⊥平面BCE;
(Ⅱ)解:过点E作EH⊥DC,
∵平面EDC⊥底面ABCD,平面EDC∩底面ABCD=DC,
∴EH⊥底面ABCD,
∵ED=EC=4,DE⊥CE,
∴DC=4
,
∴EH=2
,
∴三棱锥A-BDE的体积VA-BDE=VE-ABD=
×
×4×4
×2
=
;
(Ⅲ)过M作MG∥DE交CE于G,过G作GN∥BC交EB于N,连接MN,则
∵GN∥BC,BC∥AD,
∴GN∥AD,
∴MG∥DE,NG∩MG=G,AD∩DE=D,
∴平面MGN∥平面ADE,
∵MN?平面MGN,
∴MN∥平面ADE,
∴线段EB上存在点N,当BN=
BE时,使得MN∥平面ADE.
 (Ⅰ)证明:∵ABCD是矩形,
(Ⅰ)证明:∵ABCD是矩形,∴BC⊥DC,
∵平面EDC⊥底面ABCD,平面EDC∩底面ABCD=DC,BC⊥DC,
∴BC⊥平面EDC,
∴DE⊥BC,
∵CF⊥平面BDE,
∴ED⊥CF,
∵BC∩CF=C,DE⊥BC,ED⊥CF,
∴DE⊥平面BCE;
(Ⅱ)解:过点E作EH⊥DC,
∵平面EDC⊥底面ABCD,平面EDC∩底面ABCD=DC,
∴EH⊥底面ABCD,
∵ED=EC=4,DE⊥CE,
∴DC=4
| 2 |
∴EH=2
| 2 |
∴三棱锥A-BDE的体积VA-BDE=VE-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 32 |
| 3 |
(Ⅲ)过M作MG∥DE交CE于G,过G作GN∥BC交EB于N,连接MN,则
∵GN∥BC,BC∥AD,
∴GN∥AD,
∴MG∥DE,NG∩MG=G,AD∩DE=D,
∴平面MGN∥平面ADE,
∵MN?平面MGN,
∴MN∥平面ADE,
∴线段EB上存在点N,当BN=
| 1 |
| 3 |
点评:本题考查平面与平面垂直性质的运用,考查三棱锥A-BDE的体积,考查线面平行,考查学生分析解决问题的能力,比较综合.

练习册系列答案
相关题目
sin45°sin75°+cos75°cos45°=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知向量
=(3,4),
=(-1,5),向量k
+2
与向量
=(2,-3)垂直,则k的值是( )
| a |
| b |
| a |
| b |
| c |
| A、2 | ||
B、-
| ||
| C、1 | ||
| D、-3 |
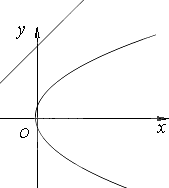 已知点P是射线y=2(x>1)上一点.过P作直线MN,交抛物线y2=4x于M,N两点,使点P平分线段MN.
已知点P是射线y=2(x>1)上一点.过P作直线MN,交抛物线y2=4x于M,N两点,使点P平分线段MN.