题目内容
若A,B,C为△ABC的三个内角,则
+
的最小值为 .
| 4 |
| A |
| 1 |
| B+C |
考点:函数的值域
专题:计算题,不等式的解法及应用
分析:由三角形的内角和定理:A+B+C=π,变形为
=1,再将
+
变形为
+
=(
+
)•
,展开并运用基本不等式即可求出最值,注意等号成立的条件.
| A+B+C |
| π |
| 4 |
| A |
| 1 |
| B+C |
| 4 |
| A |
| 1 |
| B+C |
| 4 |
| A |
| 1 |
| B+C |
| A+B+C |
| π |
解答:
解:∵A+B+C=π,
∴
=1,
∴
+
=(
+
)•
=
[4+1+
+
]
≥
(5+2
)=
.
当且仅当A=2(B+C)即A=
,取最小值为
.
故答案为:
.
∴
| A+B+C |
| π |
∴
| 4 |
| A |
| 1 |
| B+C |
| 4 |
| A |
| 1 |
| B+C |
| A+B+C |
| π |
| 1 |
| π |
| A |
| B+C |
| 4(B+C) |
| A |
≥
| 1 |
| π |
| 4 |
| 9 |
| π |
当且仅当A=2(B+C)即A=
| 2π |
| 3 |
| 9 |
| π |
故答案为:
| 9 |
| π |
点评:本题主要考查基本不等式的运用,注意等号成立的条件,同时考查三角形的内角和定理,属于中档题.

练习册系列答案
相关题目
设随机变量ξ服从正态分布N(3,4),若P(ξ<2a-2)=P(ξ>a+2),则a=( )
| A、4 | B、3 | C、2 | D、1 |
 如图,四棱锥E-ABCD,底面ABCD是矩形,平面EDC⊥底面ABCD,ED=EC=BC=4,CF⊥平面BDE,且点F在EB上.
如图,四棱锥E-ABCD,底面ABCD是矩形,平面EDC⊥底面ABCD,ED=EC=BC=4,CF⊥平面BDE,且点F在EB上.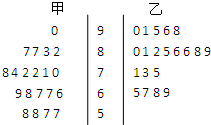 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.