题目内容
若矩阵M=
把直线l:x+y-2=0变换为另一条直线l′:x+y-4=0,试求实数a值.
|
考点:变换、矩阵的相等
专题:选作题,矩阵和变换
分析:设直线l上任意一点P(x,y)在矩阵M作用下的点P'的坐标为(x',y'),利用矩阵乘法得出坐标之间的关系,代入直线l′的方程,即可求得实数a的值;
解答:
解:设直线l上任意一点P(x,y)在矩阵M作用下的点P'的坐标为(x',y'),
则
=
,
所以
…4分
将点P'(x',y')代入直线l':x+y-4=0,
得(a-1)x+2y-4=0.
即直线l的方程为
x+y-2=0.
所以a=3. …10分.
则
|
|
|
所以
|
将点P'(x',y')代入直线l':x+y-4=0,
得(a-1)x+2y-4=0.
即直线l的方程为
| a-1 |
| 2 |
所以a=3. …10分.
点评:本题以矩阵为依托,考查矩阵的乘法,关键是正确利用矩阵的乘法公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

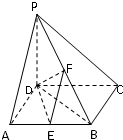 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.